Persamaan Gerak Benda Dua Dimensi, Parabola, Melingkar, Vektor, Kecepatan, Percepatan
Persamaan Gerak Benda Dua Dimensi, Parabola, Melingkar, Vektor, Kecepatan, Percepatan - Pada pecahan ini, Anda akan diajak untuk sanggup menganalisis tanda-tanda alam dan keteraturannya dalam cakupan mekanika benda titik dengan cara menganalisis gerak lurus, gerak melingkar, dan gerak parabola dengan memakai vektor. Pernahkah Anda menjentikkan uang logam dengan jari Anda? Jika Anda pernah melakukannya dan sanggup mengamati bentuk lintasan yang dibuat dikala uang logam itu bergerak, Anda akan sanggup melihat bahwa lintasan tersebut berbentuk parabola. Bentuk lintasan uang logam yang berbentuk parabola tersebut sanggup difoto memakai stroboscope, menyerupai terlihat pada gambar. Di Kelas X, Anda telah mempelajari gerak lurus dan gerak melingkar. Dalam materi pecahan ini, Anda akan mempelajari wacana gerak secara keseluruhan, yaitu gerak lurus, gerak parabola, dan gerak melingkar dengan memakai analisis vektor, perhitungan diferensial, dan integral. Setelah mempelajari materi pecahan ini, Anda akan memahami bahwa gerak parabola sanggup dianalisis melalui perpaduan antara gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB) yang arahnya saling tegak lurus. Dapatkah Anda menyebutkan contoh-contoh gerak keseharian lain yang lintasannya berbentuk parabola?
A. Persamaan Gerak Benda
Apakah yang dimaksud dengan gerak? Banyak definisi telah dikemukakan oleh para ilmuwan untuk mendeskripsikan gerak. Namun, secara Fisika Anda sanggup menyatakan bahwa gerak ditentukan alasannya ialah adanya kelajuan, kecepatan, dan percepatan benda. Seluruh kajian wacana gerak benda yang Anda pelajari akan bekerjasama dengan kedudukan benda, kecepatan, percepatan, dan waktu. Dalam membahas wacana gerak benda, seringkali benda dimisalkan sebagai partikel atau benda titik, yaitu benda yang ukurannya diabaikan dan mempunyai massa tetap (konstan). Hal ini dimaksudkan untuk memudahkan dalam mempelajari gerak benda tersebut. Di Kelas X, Anda telah mempelajari wacana gerak lurus dan gerak melingkar, serta hubungan antara gaya dan percepatan. Dalam pecahan ini, Anda akan mempelajari materi wacana gerak dengan lebih dalam memakai perhitungan vektor, diferensial, dan integral.
1. Vektor Posisi
Di Kelas X, Anda telah mempelajari bahwa besaran dalam Fisika digolongkan ke dalam dua kelompok, yaitu besaran skalar dan besaran vektor. Besaran skalar ialah besaran yang hanya mempunyai nilai saja, sedangkan besaran vektor ialah besaran yang mempunyai nilai dan arah. Bandingkanlah kedua pernyataan berikut. Mobil Ali bergerak dengan kecepatan 60 km/jam ke utara. Mobil Budi bergerak dengan kelajuan 60 km/jam. Manakah dari dua pernyataan tersebut yang merupakan besaran vektor? Kecepatan mempunyai besar dan arah sehingga disebut sebagai besaran vektor, sedangkan kelajuan hanya mempunyai besar saja sehingga disebut sebagai besaran skalar. Apabila benda dianggap sebagai benda titik, atau partikel, posisi benda tersebut pada suatu bidang sanggup dinyatakan dengan vektor posisi r, yaitu sebuah vektor yang ditarik dari titik asal hingga ke posisi titik tersebut berada. Vektor posisi r suatu partikel pada bidang xy sanggup dinyatakan sebagai berikut.
r = xi + yj (1–1)
dengan (x, y) ialah koordinat partikel, sementara i dan j ialah vektor satuan yang menyatakan arah pada sumbu-x dan sumbu-y. Vektor satuan mempunyai nilai 1 satuan.
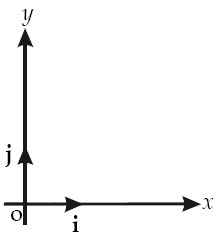 |
| Gambar 1. Vektor satuan i pada arah sumbu-x dan vektor satuan j pada arah sumbu-y. |
 |
| Gambar 2. Posisi titik A dinyatakan dalam vektor posisi dengan rA = xi + yj . |
Untuk lebih jelasnya, perhatikanlah Gambar 3. berikut.
 |
| Gambar 3. Posisi titik A apabila dinyatakan dalam vektor posisi rA=(5i + 3j) cm. |
Posisi partikel A di bidang xy ialah pada x = 5 cm dan y = 3 cm, atau pada koordinat (5, 3). Vektor posisi partikel A dinyatakan sebagai berikut :
rA = xAi + yAj = (5i + 3j) cm.
2. Perpindahan
Perpindahan ialah perubahan posisi (kedudukan) suatu benda dalam waktu tertentu. Sebuah partikel berpindah dari titik P ke titik Q berdasarkan lintasan kurva PQ, menyerupai pada Gambar 4.
 |
| Gambar 4. Garis putus-putus menyatakan lintasan partikel. Perpindahan posisi partikel dari posisi awal di titik P ke posisi titik Q dinyatakan dengan Δr.. |
Apabila posisi titik P dinyatakan sebagai rP dan posisi titik Q dinyatakan sebagai rQ maka perpindahan yang terjadi dari titik P ke titik Q tersebut ialah vektor Δ r, yaitu :
Δr = rQ – rP (1–2)
Persamaan (1–2) jikalau diubah dalam kalimat sanggup dinyatakan bahwa perpindahan suatu benda sama dengan posisi selesai benda dikurangi posisi awal.
Bagaimanakah cara memilih besar perpindahan yang dilakukan oleh partikel tersebut? Setiap benda membutuhkan waktu untuk berpindah atau mengubah kedudukannya. Dalam masalah perpindahan tersebut, pada dikala t = t1, partikel berada di titik P dengan vektor posisinya rP. Pada dikala t = t2, partikel berada di titik Q dengan vektor posisinya rQ.
Kemudian, apabila rP= (xPi + yPj) dan rQ = (xQi + yQj), Persamaan (1–2) sanggup dituliskan menjadi rPQ = (xQi + yQj) – (xPi + yPj) = (xQ – xP)i + (yQ – yP)j.
Apabila xQ – xP = Δx dan yQ – yP = Δy, serta perpindahan yang dilakukan partikel rPQ dinyatakan sebagai Δr, Persamaan (1–2) bermetamorfosis :
Δr = Δxi + Δyj (1–3)
Oleh alasannya ialah besar perpindahan partikel Δr sama dengan panjang vektor Δr maka sanggup dituliskan :
Arah perpindahan partikel sanggup ditentukan dari besar sudut yang dibuat oleh vektor perpindahan Δr terhadap sumbu-x. Perhatikanlah Gambar 5 berikut.
 |
| Gambar 5. Perpindahan vektor Δ r berdasarkan sumbu-x ialah sebesar Δ x dan berdasarkan sumbu-y sebesar Δ y. |
Apabila sudut yang dibuat oleh vektor perpindahan Δr terhadap sumbu-x ialah θ , arah perpindahan vektor Δr dinyatakan sebagai :
Contoh Soal 1 :
Sebuah titik materi bergerak dari titik P (3, 2) ke titik Q (11, 8). Tuliskanlah vektor posisi titik itu ketika berada di titik P dan di titik Q. Hitunglah vektor perpindahan dari titik P ke titik Q serta besar dan arah vektor perpindahan tersebut.
Kunci Jawaban :
Diketahui: koordinat di titik P (3, 2) dan di titik Q (11, 8). Vektor posisi di titik P (rP) dan vektor posisi di titik Q (rQ) ialah :
rP = 3i + 2j
rQ = 11i + 8j
Vektor perpindahan dari titik P ke titik Q ialah Δr yang diperoleh sebagai berikut :
Δr = rQ – rP = (11i + 8j) – (3i + 2j)
Δr = 8i + 6j
Besar vektor Δr ialah :
Arah perpindahan vektor itu ialah :
tanθ = Δy / Δx = 6/8 = 3/4
sehingga θ = 37°
Jadi, vektor perpindahan ialah Δr = 8i + 6j, panjang perpindahannya 10 satuan, dan sudut arah perpindahannya 37° terhadap arah sumbu-x positif. Untuk lebih jelasnya, perhatikanlah gambar berikut.
3. Kecepatan Rata-Rata dan Kecepatan Sesaat
Secara matematis, kecepatan didefinisikan sebagai perubahan posisi per satuan waktu. Di Kelas X, Anda telah mempelajari wacana kecepatan yang terbagi atas kecepatan rata-rata dan kecepatan sesaat. Sekarang, Anda akan membahas analisis mengenai kedua jenis kecepatan tersebut ditinjau dari perhitungan vektor.
a. Kecepatan Rata-Rata
Perhatikanlah Gambar 6. Posisi benda di titik P pada dikala t dinyatakan sebagai r. Kemudian, benda tersebut berpindah selama selang waktu Δt sejauh Δr sehingga pada dikala t + Δt, benda berada di titik Q dengan posisi r + Δr.
 |
| Gambar 6. Sebuah benda berpindah secara linear dari titik P ke titik Q. |
Berdasarkan Persamaan (1–3) sanggup dituliskan perpindahan posisi benda ialah sebagai berikut.
Δr = (r + Δr) – r
Berdasarkan definisi matematis kecepatan, sanggup dituliskan
dengan :
disebut kecepatan rata-rata. Kecepatan rata-rata benda dalam arah sumbu-x dan sumbu-y sanggup dicari dengan cara memasukkan nilai Δr dari Persamaan (1–3) sebagai berikut.
Perhatikanlah Gambar 7. Gambar tersebut menunjukkan grafik perpindahan benda dari titik P ke titik Q berdasarkan sumbu-x.
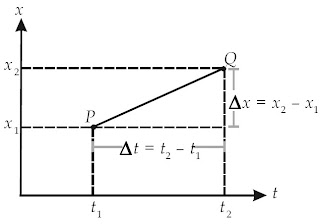 |
| Gambar 7. Apabila gerak benda hanya pada arah sumbu-x maka kecepatan rata-rata benda v x ialah kemiringan garis yang menghubungkan titik P dengan titik Q, yaitu Δx/Δt |
Dari grafik tersebut sanggup dilihat bahwa selama selang waktu Δt, benda berpindah sejauh Δx. Oleh alasannya ialah itu, kecepatan rata-rata benda dalam arah sumbu-x, yaitu Δx/Δt dituliskan dengan lambang,  . Apabila benda tersebut juga berpindah berdasarkan sumbu-y, kecepatan rata-rata benda dalam arah sumbu-y, yaitu Δy/Δt. dituliskan dengan lambang
. Apabila benda tersebut juga berpindah berdasarkan sumbu-y, kecepatan rata-rata benda dalam arah sumbu-y, yaitu Δy/Δt. dituliskan dengan lambang  .Dengan demikian, kecepatan rata-rata sebuah benda pada bidang xy sanggup dituliskan sebagai berikut :
.Dengan demikian, kecepatan rata-rata sebuah benda pada bidang xy sanggup dituliskan sebagai berikut :
Besar kecepatan rata-rata benda sanggup dihitung memakai persamaan berikut.
b. Kecepatan Sesaat
Kecepatan sesaat suatu benda sanggup diketahui dengan cara menghitung kecepatan rata-rata benda tersebut untuk selang waktu yang sangat singkat atau Δt mendekati nol. Penulisannya secara matematis ialah sebagai berikut.
Perhatikanlah Gambar 8. berikut.
 |
| Gambar 8. Grafik x terhadap t untuk selang waktu Δt yang semakin kecil. |
Dari gambar tersebut, sanggup Anda lihat bahwa kemiringan garis yang menyatakan kecepatan rata-rata suatu benda akan semakin curam apabila selang waktu perpindahannya semakin kecil. Oleh alasannya ialah itu, kecepatan sesaat sanggup didefinisikan sebagai kemiringan garis tangensial pada titik P, yaitu turunan posisi terhadap waktu.
Pada Gambar 8, kecepatan sesaatnya secara matematis dituliskan sebagai berikut.
Dalam kajian vektor, kecepatan sesaat benda yang bergerak berdasarkan sumbu-x dan sumbu-y dinyatakan sebagai berikut.
Oleh karena dx/dt = vx dan dyx/dt = vy maka Persamaan (1–12) sanggup dituliskan menjadi :
v = vxi + vyj (1–13)
Besarnya kecepatan sesaat atau kelajuan rata-rata benda sanggup dihitung dengan memakai persamaan berikut.
Perhatikanlah Gambar 9. Dari grafik kecepatan terhadap waktu benda di titik P yang mempunyai kecepatan v, arah kecepatan benda di titik tersebut terhadap sumbu-x dinyatakan dengan θ .
 |
| Gambar 9. Arah percepatan v di titik P terhadap sumbu-x positif. |
Besar θ secara matematis, sanggup diperoleh sebagai berikut :
dengan: vx = v cosθ, dan vy = v sinθ.
Catatan Fisika :
dr/dt, dx/dt, dan dy/dt disebut fungsi turunan posisi (r, x, atau y) terhadap waktu t.
Rumus fungsi turunan:
contoh:
Catatan Fisika :
Pada buku ini, besaran vektor ditulis dengan aksara tebal dan miring, contohnya: r, v, a. Adapun, vektor satuan ditulis dengan aksara tebal dan tegak, contohnya: i, j, dan k.
Contoh Soal 2 :
Sebuah partikel sedang bergerak pada suatu bidang dengan sumbu koordinat x dan y. Posisi partikel berubah terhadap waktu mengikuti persamaan r = (6 + 3t)i + (8 + 4t)j dengan r dalam meter dan t dalam sekon. Tentukanlah:
a. perpindahan partikel dalam selang waktu t = 0 hingga t = 2 sekon;
b. besar kecepatan rata-rata partikel dalam selang waktu t = 0 hingga t = 2 sekon;
c. besar dan arah kecepatan partikel pada dikala t = 2 sekon.
Kunci Jawaban :
Diketahui: vektor posisi partikel, yaitu r = (6 + 3t)i + (8 + 4t)j.
a. t1 = 0 sekon adalah r1 = [6 + (3)(0)]i + [8 + (4)(0)]j = (6i + 8j) meter.
t2 = 2 sekon adalah r2 = [6 + (3)(2)]i + [8 + (4)(2)]j = (12i + 16j) meter.
Perpindahan partikel dari t1 = 0 sekon hingga t2 = 2 sekon ialah :
Δr = r2 – r1 = (12i + 16j) – (6i + 8j) = (6i + 8j) meter
Besar vektor Δr ialah :
b. Kecepatan rata-rata partikel ialah :
Besar kecepatan rata-rata partikel ialah :
Vektor kecepatan partikel sebagai fungsi waktu ditentukan sebagai berikut.
vx = dx/dt = d/dt (6 + 3t) = 3 m/s
vy = dy/dt = d/dt (8 + 4t) = 4 m/s
Dengan demikian, diperoleh vektor kecepatan sesaat partikel ialah :
v = vxi + vyj = (3i + 4j) m/s.
Besar kecepatan sesaat partikel ialah :
Arah vektor kecepatan sesaat terhadap sumbu-x ialah θ dengan :
tanθ = vy/vx = 4/3
θ = 53°.
Contoh Soal 3 :
Perhatikan grafik kedudukan (x) terhadap waktu (t) berikut.
Tentukanlah kecepatan rata-rata benda dalam selang waktu:
a. antara t = 0 hingga t = 3 s;
b. antara t = 3 hingga t = 8 s; dan
c. antara t = 8 hingga t = 12 s.
Kunci Jawaban :
Diketahui: grafik x–t dan kecepatan rata-rata ialah :
a. Kecepatan rata-rata benda antara t = 0 hingga t = 3 s ialah :
b. Kecepatan rata-rata benda antara t = 3 hingga t = 8 s ialah :
c. Kecepatan rata-rata benda antara t = 8 hingga t = 12 s ialah :
Tokoh Fisika :
Galileo Galilei
Galileo lahir di Pisa, Italia. Pada umur 19 tahun, ia mempelajari matematika dan menyebarkan penelitiannya wacana gerak mekanik, terutama mengenai gerak di bidang miring, gerak pendulum, dan gerak jatuh bebas. Saat mengajar di Universitas Padua, ia menjadi penyokong teori Copernicus mengenai sistem Matahari, yang bertentangan dengan teori yang diakui dikala itu. Saat menerbitkan karyanya, ia disidang untuk menyangkal hasil penelitiannya, namun ia tetap yakin dengan penelitiannya dan tidak mau menyerah. Setelah ia dijatuhi eksekusi tahanan rumah, ia meninggal pada umur 78 tahun. Walaupun begitu, ia menuntaskan penelitiannya mengenai gerak. Karya tulisnya, kemudian diselundupkan dari Italia dan diterbitkan di Belanda. (Sumber: www.hao.ucar.edu).
4. Menetukan Posisi dari Fungsi Kecepatan
Fungsi posisi suatu benda, yaitu koordinat benda (x, y) sanggup diperoleh dengan cara mengintegralkan persamaan kecepatan benda sebagai fungsi waktu.
Dalam arah sumbu-x, fungsi posisi benda diturunkan sebagai berikut.
vx = dy/dt atau dy = vxdt
Posisi x ditentukan dengan :
Dalam arah sumbu-y, fungsi posisi benda diturunkan sebagai berikut.
vy = dy/dt atau dy = vydt
Posisi y ditentukan dengan :
(x0, y0) menyatakan koordinat posisi awal benda, sedangkan (x, y) menyatakan koordinat posisi benda sehabis bergerak dalam selang waktu t.
Apabila dituliskan dalam bentuk vektor, posisi benda sanggup dituliskan sebagai berikut :
r = xi + yj
atau
Secara matematis, integral ialah penjumlahan yang kontinu. Dengan demikian, posisi benda sanggup ditentukan dengan metode grafik sebagai berikut. Apabila kecepatan sebuah benda dinyatakan dengan persamaan vx = 2t + 5, posisi benda ialah :
Misalkan, batas integral ialah dari t = 0 hingga dengan t = 2. Dengan memasukkan nilai batas integral, didapatkan perpindahan benda ialah :
Cara lain untuk memilih perpindahan benda ialah dengan menghitung luas kawasan di bawah kurva v(t).
 |
| Gambar 10. Luas kawasan yang diarsir menyatakan besar perpindahan yang dilakukan benda dalam selang waktu t = 0 hingga dengan t = 2. |
Contoh Soal 4 :
Sebuah kendaraan beroda empat dengan kecepatan 36 km/jam direm mendadak sehingga terbentuk bekas di jalan sepanjang 20 m. Waktu pengereman yang dibutuhkan hingga kendaraan beroda empat tersebut berhenti ialah ....
a. 2 s
b. 4 s
c. 6 s
d. 8 s
e. 10 s
Kunci Jawaban :
Diketahui:
v0 = 36 km/jam = 10 m/s
Δr = luas segitiga
maka,
20 = (½) (t) (10)
t = 4 s
Jawab: d
Dengan demikian, sanggup disimpulkan bahwa besar perpindahan benda sama dengan luas di bawah kurva kecepatan sebagai fungsi waktu v(t). Secara matematis dituliskan sebagai berikut.
Contoh Soal 5 :
Sebuah benda bergerak pada bidang xy. Pada posisi awal, benda berada pada koordinat (3,2) m. Komponen-komponen kecepatan benda memenuhi persamaan vx = 12 + 4t dan vy = 9 + 3t dengan vx dan vy dalam m/s, dan t dalam sekon.
Tentukanlah:
a. persamaan umum vektor posisi benda,
b. posisi benda pada dikala t = 3 sekon, dan
c. perpindahan benda antara t = 1 sekon dan t = 3 sekon.
Kunci Jawaban :
Diketahui: posisi awal benda (3, 2) m, vx = 12 + 4t, dan vy = 9 + 3t.
a. Posisi awal benda (3,2) m maka x0 = 3 m dan y0 = 2 m. Dengan demikian, diperoleh :
r = (3 + 12t + 2t2)i + (2 + 9t + 3/2 t2)j
b. Posisi benda pada dikala t = 3 sekon ialah :
x = 3 + (12) (3) + (2) (32) = 57 m
y = 2 + (9) (3) + (3/2) (32) = 42,5 m
Jadi, pada dikala t = 3 sekon vektor posisi benda sanggup dituliskan sebagai
r = (57i + 42,5j ) meter.
c. Pada t1 = 1 sekon maka r1 = [3 + (12)(1) + (2)(12)]i + [2 + (9)(1) + (3/2 )(12)]j = (17i + 12,5j) meter
Pada t2 = 3 sekon maka r2 = [3 + (12)(3) + (2)(32)]i + [2 + (9)(3) + (3/2)(32)]j = (57i + 42,5j) meter
Perpindahan partikel dari t1 = 1 sekon hingga t2 = 3 sekon adalah
Δr = r2 – r1 = (57i + 42,5j) – (17i + 12,5j) = (40i + 30j) meter
Besar vektor Δr ialah :
5. Percepatan Rata-Rata dan Percepatan Sesaat
Percepatan ialah perubahan kecepatan per satuan waktu. Perubahan kecepatan per satuan waktu yang bernilai positif disebut percepatan, sedangkan yang bernilai negatif disebut perlambatan. Sebagaimana halnya dengan kecepatan, pembahasan percepatan juga terbagi atas dua, yaitu percepatan rata-rata dan percepatan sesaat.
a. Percepatan Rata-Rata
Perhatikanlah Gambar 12.
Grfaik kecepatan terhadap waktu pada gambar tersebut menyatakan gerak benda yang berpindah dengan kecepatan tertentu setiap saatnya. Apabila pada dikala t kecepatan benda ialah v dan pada dikala t +Δt kecepatannya v + Δv, percepatan rata-rata benda tersebut (ā) dinyatakan sebagai berikut.
Penulisan Persamaan (1–19) dalam bentuk vektor dalam arah sumbu-x dan sumbu-y ialah sebagai berikut.
Oleh alasannya ialah :
Persamaan (1–20) sanggup ditulis menjadi :
Besar percepatan rata-rata dinyatakan sebagai :
Arah percepatan rata-rata sanggup dituliskan sebagai berikut.
b. Percepatan Sesaat
Percepatan sesaat merupakan kecepatan rata-rata untuk selang waktu Δt yang sangat kecil atau mendekati nol. Secara matematis, persamaannya dituliskan sebagai berikut.
Apabila vektornya diadaptasi berdasarkan arah sumbu-x dan sumbu-y, Persamaan (1–24) bermetamorfosis :
Oleh alasannya ialah v = dr/dt maka Persamaan (1–25) sanggup dituliskan sebagai berikut :
Catatan Fisika :
Jatuh Bebas
Dahulu orang percaya pada gagasan Aristoteles mengenai benda jatuh, yaitu benda yang lebih berat akan lebih dulu mencapai tanah dibandingkan benda yang lebih ringan. Melalui percobaannya dengan mengukur waktu tempuh bola-bola yang digelindingkan pada suatu bidang miring, Galileo membantah gagasan Aristoteles tersebut. Dari hasil percobaannya, Galileo berkesimpulan bahwa waktu yang dibutuhkan kedua benda jatuh untuk mencapai tanah ialah sama. (Sumber: Jendela Iptek, 1997)
Contoh Soal 6 :
Sebuah partikel bergerak dengan fungsi kecepatan v(t) = 2t2 – 3t + 10 jikalau v dinyatakan dalam m/s dan t dalam sekon, tentukanlah:
a. percepatan rata-rata partikel untuk selang waktu t = 2 sekon hingga t = 4 sekon,
b. percepatan awal partikel, dan
c. percepatan partikel pada dikala t = 6 sekon.
Kunci Jawaban :
Diketahui: v(t) = 2t2 – 3t + 10.
Persamaan umum kecepatan ialah v(t) = 2t2 – 3t + 10 sehingga :
untuk t2 = 4 sekon, v2 = 2(4)2 – 3(4) + 10 = 30 m/s
untuk t1 = 2 sekon, v1 = 2(2)2 – 3(2) + 10 = 12 m/s
Diperoleh :
b. Persamaan umum percepatan sesaat diperoleh sebagai turunan pertama dari fungsi kecepatan, yaitu:
Percepatan awal partikel ialah percepatan pada t = 0 sehingga :
a = 4(0) – 3 = –3 m/m2.
c. Percepatan partikel pada dikala t = 6 sekon adalah
a = 4(6) – 3 = 21 m/m2.
Contoh Soal 7 :
Sebuah kendaraan beroda empat bergerak dengan grafik kecepatan (v) terhadap waktu (t) menyerupai terlihat pada gambar di bawah ini.
Tentukanlah:
a. percepatan rata-rata benda antara t = 0 sekon hingga t = 4 sekon, dan
b. percepatan rata-rata benda antara t = 4 sekon hingga t = 8 sekon
Kunci Jawaban :
Diketahui: grafik v – t.
a. Percepatan rata-rata benda antara t = 0 hingga t = 4 sekon, yaitu :
b. Percepatan rata-rata benda antara t = 4 hingga t = 8 sekon, yaitu :
6. Menentukan Kecepatan dari Fungsi Percepatan
Fungsi kecepatan sanggup diperoleh dari fungsi percepatan dengan metode integral, yaitu :
atau :
Secara matematis, integral ialah penjumlahan yang kontinu. Metode yang dipakai untuk memeroleh nilai kecepatan dari fungsi percepatan sanggup dilakukan dengan analogi pada cara untuk mendapat nilai perpindahan dari fungsi kecepatan. Perhatikan Gambar 13. Kecepatan partikel secara grafik sanggup ditentukan sebagai berikut.
 |
| Gambar 13. Luas kawasan yang diarsir menyatakan besar kecepatan yang dilakukan benda dalam selang waktu t. |
Besar kecepatan = luas kawasan di bawah kurva a (t)
Contoh Soal 8 :
Sebuah benda bergerak dengan kecepatan awal 3 m/s. Jika benda mengalami percepatan a (t) = (4t –2) m/s2, tentukanlah:
a. persamaan kecepatan benda, dan
b. kecepatan benda pada t = 2 sekon.
Kunci Jawaban :
Diketahui: vo = 3 m/s dan a(t) = (4t – 2) m/s2.
a. Kecepatan sanggup diperoleh dari fungsi percepatan dengan metode integral.
v = v0 + ∫ a dt = 3 + ∫ (4t – 2) dt = (3 + 2t2 – 2t) m/s2.
b. Kecepatan benda pada dikala t = 2 sekon adalah
v = 3 + (2)(2)t2 – (2)(2) = 7 m/s.
7. Gerak Lurus Beraturan dan Gerak Lurus Berubah Beraturan
Di Kelas X, Anda telah mengenal dan mempelajari dua jenis gerak lurus, yaitu gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB). Pada gerak lurus beraturan, kecepatan gerak benda tetap dan percepatan benda sama dengan nol. Persamaan geraknya diperoleh melalui persamaan:
Pada GLB, nilai v tetap dan tidak bergantung pada waktu sehingga persamaan sanggup dituliskan menjadi:
s = s0 + vt (1–28)
dengan s0 merupakan jarak tempuh benda pada dikala t = 0.
Pada gerak lurus berubah beraturan (GLBB), benda bergerak dengan percepatan tetap. Persamaan geraknya diperoleh melalui :
Pada GLBB, nilai a tetap dan tidak bergantung waktu sehingga persamaan sanggup dituliskan menjadi :
Dengan demikian, diperoleh persamaan sebagai berikut.
vt = v0 + at (1–29)
atau,
Apabila Persamaan (1–29) diintegralkan, akan diperoleh jarak tempuh benda, yaitu :
Oleh alasannya ialah v(t) = v0 + at maka :
Jika s0 = 0, akan diperoleh persamaan :
Kemudian, jikalau Persamaan (1–30) disubstitusikan ke Persamaan (1–32) diperoleh :
2as = 2v0 vt – 2v02 + vt2 – 2v0 vt + v02
vt2 = v02 + 2as (1–33)
Contoh Soal 9 :
Besar kecepatan suatu partikel yang mengalami perlambatan konstan ternyata berubah dari 30 m/s menjadi 15 m/s sehabis menempuh jarak sejauh 75 m. Setelah menempuh jarak berapa lagi partikel tersebut berhenti?
Kunci Jawaban :
B. Gerak Parabola
Perhatikanlah lintasan yang dibuat oleh bola basket yang dilemparkan ke dalam ring pada Gambar 14.
Lintasan bola basket tersebut berbentuk parabola. Gerak yang lintasannya berbentuk parabola disebut gerak parabola. Contoh umum gerak parabola ialah gerak benda yang dilemparkan ke atas membentuk sudut tertentu terhadap permukaan tanah. Gerak parabola sanggup dipandang dalam dua arah, yaitu arah vertikal (sumbu-y) yang merupakan gerak lurus berubah beraturan (GLBB), dan arah horizontal (sumbu-x) yang merupakan gerak lurus beraturan (GLB). Perhatikan Gambar 15. berikut.
 |
| Gambar 14. Lintasan bola basket dikala dilemparkan ke dalam ring akan berbentuk parabola. |
Gerak pada sumbu-x (horizontal) ialah gerak lurus beraturan alasannya ialah kecepatan benda di setiap titik bernilai konstan dan berlaku persamaan
vx = v0x = v0 cosα (1–34)
Adapun, jarak mendatar yang ditempuh oleh sebuah benda ditentukan oleh persamaan :
x = vx t = v0cosα t (1–35)
Gerak pada sumbu-y (vertikal) ialah gerak lurus berubah beraturan, alasannya ialah benda mengalami perubahan kecepatan akhir percepatan gravitasi Bumi. Dalam hal ini, arah gerak benda vertikal ke atas sehingga persamaan kecepatan geraknya pada setiap titik ialah :
vy = v0y – gt (1–36)
oleh karena v0y = v0 sinα , Persamaan (1–36) sanggup dituliskan menjadi :
vy = v0 sinα – gt (1–37)
Posisi benda pada sumbu-y (menurut ketinggian) sanggup dituliskan dengan persamaan berikut :
atau :
1. Kecepatan dan Arah Kecepatan Benda di Sembarang Titik
Pada gerak parabola, benda mempunyai kecepatan pada komponen sumbu-x dan sumbu-y sehingga besar kecepatan benda di sembarang titik secara matematis, dirumuskan sebagai berikut.
Arah kecepatan benda terhadap sumbu mendatar (sumbu-x) dirumuskan sebagai berikut.
Oleh alasannya ialah nilai vx selalu positif maka positif atau negatifnya sudut θ bergantung pada nilai vy.
2. Beberapa Persamaan Khusus pada Gerak Parabola
Persamaan-persamaan khusus gerak parabola ini hanya berlaku untuk gerak parabola dengan lintasan dari tanah, kemudian kembali lagi ke tanah menyerupai pada Gambar 16.
 |
| Gambar 16. Lintasan gerak parabola benda dengan titik tertinggi di B dan titik terjauh di C. |
Pada pola gerak parabola tersebut, suatu benda bergerak dari titik A dengan kecepatan awal v0 dan sudut θ . Benda tersebut mencapai titik tertinggi di titik B dan jarak terjauh di titik C.
a. Waktu untuk Mencapai Titik Tertinggi (Titik B)
Pada dikala benda yang melaksanakan gerak parabola mencapai titik tertinggi, kecepatan benda pada komponen vertikal (sumbu-y) vy = 0. Persamaannya ialah sebagai berikut.
vy = v0y – gtAB
0 = v0 sinα – gtAB
gtAB = v0 sinα Ketinggian benda di titik tertinggi ialah H = ½ g(tBC)2. Sifat simetri grafik parabola menunjukkan bahwa waktu yang diharapkan benda untuk mencapai titik tertinggi dari posisi awal (tAB), sama dengan waktu tempuh benda dari titik tertinggi ke jarak terjauh (tBC). Dengan demikian, akan diperoleh persamaan :
b. Tinggi Maksimum (H )
Tinggi maksimum benda yang melaksanakan gerak parabola sanggup ditentukan dari penurunan Persamaan (1–43) sebagai berikut.
dikuadratkan menjadi :
c. Jarak Terjauh (X )
Waktu tempuh untuk mencapai titik terjauh (titik C) sama dengan dua kali waktu yang diharapkan untuk mencapai titik tertinggi (tAC = 2 tAB). Jarak terjauh yang dicapai benda pada sumbu-x (dilambangkan dengan X) ialah :
Menurut trigonometri, 2 sinα cosα = sin2α sehingga persamaan untuk jarak terjauh yang sanggup dicapai benda sanggup dituliskan :
Perbandingan antara jarak terjauh (X) dan tinggi maksimum (H) akan menghasilkan persamaan :
Catatan Fisika :
dari rumus trigonometri, diketahui : sin2α = 2 sinα cosα
Contoh Soal 10 :
Sebuah peluru ditembakkan dengan kecepatan 60 m/s dan sudut elevasi 30°. Ketinggian maksimum yang dicapai peluru ialah ....
a. 30 m
b. 45 m
c. 50 m
d. 90 m
e. 100 m
Kunci Jawaban :
Diketahui:
v0 = 60 m/s
α = 30°
g = 10m/s2
H = 45 m
Contoh Soal 11 :
Dari titik A di tanah, sebuah bola dilemparkan dengan kecepatan awal 20 m/s dan sudut elevasi 37° (sin 37° = 0,6). Jika g = 10 m/s2, hitunglah:
a. komponen kecepatan awal dalam arah horizontal dan vertikal,
b. kecepatan bola sehabis 0,4 sekon,
c. posisi bola sehabis 0,4 sekon,
d. tinggi maksimum yang sanggup dicapai bola, dan
e. jarak lemparan terjauh yang dicapai bola.
Kunci Jawaban :
Diketahui: v0 = 20 m/s, α = 37°, dan g = 10 m/s2.
a. Komponen kecepatan awal
1) Dalam arah horizontal
v0x = v0 cosα = (20 m/s)(cos 37°)
v0x = (20 m/s)(0,8) = 16 m/s.
2) Dalam arah vertikal
v0y = v0 sinα = (20 m/s)(sin 37°)
v0y = (20 m/s)(0,6) = 12 m/s.
b. Kecepatan bola sehabis 0,4 s (t = 0,4 s)
1) Kecepatan dalam arah horizontal tetap, yaitu
vx = v0x = 16 m/s.
2) Kecepatan dalam arah vertikal
vy = v0y – gt = 12 m/s – (10 m/s2)(0,4 s) = 8 m/s.
Dengan demikian diperoleh :
c. Posisi bola sehabis 0,4 s
1) Posisi pada arah horizontal
x = vxt = (16 m/s)(0,4 s) = 6,4 m.
2) Posisi pada arah vertikal :
y = (12 m/s)(0,4 s) – (½)(10 m/s2)(0,4 s)2
y = 5,6 m.
Dengan demikian, posisi bola sehabis 0,4 s berada pada koordinat (6,4 m ; 5,6 m).
d. Tinggi maksimum yang dicapai bola
e. Jarak lemparan terjauh yang dicapai bola
X = = 38,4 m
Catatan Fisika :
Penduduk di Pulau Nias mempunyai tradisi unik. Seorang cowok Nias remaja atau menginjak remaja harus bisa meloncati kerikil yang tingginya sekitar 2 meter, sebagai tanda keberanian, kedewasaan, dan kesatriaan. Gerak yang dilakukan oleh cowok Nias ini merupakan salah satu pola gerak parabola yang telah dikenal semenjak dulu oleh para penduduk Nias. Dalam menuntaskan tantangan loncat kerikil ini, loncatan yang dibuat peloncat harus mempunyai kecepatan awal tertentu, tinggi maksimum, dan rentang maksimum, sebagaimana yang telah Anda pelajari dalam materi gerak parabola. (Sumber: www.geocities.com)
Contoh Soal 12 :
Sebuah benda dilemparkan dari puncak sebuah gedung yang tingginya 40 m. Kecepatan awal benda 20 m/s dengan sudut elevasi 30°. Tentukan jarak terjauh dalam arah mendatar yang sanggup dicapai benda, dihitung dari dasar gedung.
Kunci Jawaban :
Diketahui: h= 40 m, v0 = 20 m/s, dan θ = 30°.
Perhatikan gambar.
Untuk memilih jarak terjauh dalam arah mendatar (X), lebih dahulu Anda hitung waktu yang diharapkan benda untuk bergerak dari A ke B. Waktu ini bisa dihitung dari gerak vertikal ke atas (sumbu-y) sebagai berikut:
v0y = v0 sin 30° = (20 m/s) (½) = 10 m/s
–40 = 10t – () (10)t2; bagi 5
–8 = 2t – t2
0 = t2 – 2t – 8
0 = (t + 2) (t – 4)
Diperoleh :
t = –2 s (tidak digunakan)
t = 4 s
Dari gerak horizontal (sumbu -x), diperoleh
x = v0t cos 30°
Catatan Fisika :
nilai y diambil harga negatif (–40) alasannya ialah posisi selesai (titik B) berada di bawah posisi asal (titik A).
Contoh Soal 13 :
Sebuah kendaraan beroda empat hendak menyeberangi sebuah parit yang lebarnya 4 m. Perbedaan tinggi antara kedua sisi parit itu ialah 15 cm, menyerupai ditunjukkan pada gambar. Jika percepatan gravitasi 10 m/s2, berapakah kelajuan (v) minimum biar penyeberangan kendaraan beroda empat sanggup sempurna berlangsung?
Kunci Jawaban :
Perhatikan kembali gambar. Dari gambar diketahui: y = 0,15 m, x = 4 m, v0x= v, v0y = 0, dan g = 10 m/s2.
Pada masalah tersebut, gerak kendaraan beroda empat merupakan perpaduan antara GLB pada arah mendatar dan GLBB (gerak jatuh bebas) dalam arah vertikal. Oleh alasannya ialah itu, diperoleh
1) Dari gerak jatuh bebas diperoleh waktu untuk datang di sisi parit pecahan bawah sebagai berikut:
y = 0,173 s.
2) Dari gerak horizontal diperoleh kelajuan v sebagai berikut :
Jadi, kelajuan minimum biar penyeberangan kendaraan beroda empat sanggup sempurna berlangsung ialah v = 23 m/s.
Percobaan Fisika Sederhana 1 :
Membandingkan Waktu Tempuh Benda pada Gerak Jauh Bebas dan Gerak Parabola
Alat dan Bahan
- Penggaris plastik
- Karton tebal
- Dua uang logam (koin)
- Selotip
Prosedur
 |
| (a) Karton tebal yang telah dilipat. (b) Lipatan karton tebal yang telah dipasangkan pada penggaris dan ditempati 2 keping uang logam. (c) Penggaris yang dilengkungkan sebelum dilepaskan. |
- Lipatlah karton tebal menjadi menyerupai aksara ''T'' terbalik dan pasangkan pada penggaris plastik dengan memakai selotip. Kemudian, letakkan satu uang logam (koin) di setiap sisi karton. Perhatikanlah gambar.
- Lengkungkanlah penggaris plastik, kemudian lepaskan. Koin yang berada di depan akan mengalami gerak parabola, sedangkan koin yang berada di belakang akan mengalami gerak jatuh bebas.
- Dengarkanlah suara yang timbul dikala kedua koin tersebut jatuh dari penggaris plastik. Apakah yang sanggup Anda simpulkan?
- Diskusikanlah kesimpulan Anda dengan teman sebangku dan guru Fisika Anda.
3. Persamaan Vektor Gerak Parabola
Menurut analisis vektor, persamaan-persamaan gerak parabola sanggup dituliskan sebagai berikut. Vektor posisi pada gerak parabola ialah :
r = xi + yj
r = (v0 cosα t)i + (v0 sinα t –½ gt 2)j (1–47)
Vektor kecepatan gerak parabola adalah
v = vxi + vy j
v = (v0 cosα )i + (v0 sinα – gt 2)j (1–48)
Dalam kehidupan sehari-hari, Anda banyak menjumpai pola gerak melingkar. Bumi berputar mengelilingi Matahari dalam orbit yang mendekati lingkaran, demikian juga satelit-satelit yang bergerak dalam orbit melingkar mengelilingi Bumi.
Mobil yang bergerak mengitari suatu sudut juga bergerak dalam busur melingkar. Kajian wacana gerak melingkar telah Anda pelajari di Kelas X. Dalam subbab ini, pembahasan gerak melingkar akan ditinjau secara umum memakai fungsi turunan dan integral.
Contoh Soal 14 :
Posisi peluru yang ditembakkan di atas bidang datar dengan sudut elevasi tertentu dinyatakan oleh persamaan r = [80ti + (60t – 5t2)j] m. Jika i dan j menyatakan vektor satuan dalam arah x dan y, serta t dalam sekon, tentukanlah:
a. kecepatan awal peluru,
b. sudut elevasi tembakan,
c. kecepatan peluru di titik tertinggi,
d. waktu untuk mencapai jarak maksimum, dan
e. jarak mendatar maksimum tembakan.
Kunci Jawaban :
Diketahui: r [80ti + (60t – 5t2)j] m
a. Kecepatan awal peluru (t = 0),
v = dr/dt = 80i + (60 – 10t)j
Pada t = 0 diperoleh :
v0 = 80i + 60j
b. Sudut elevasi tembakan (α )
α =37°
c. Kecepatan peluru di titik tertinggi vy = 0 sehingga peluru hanya mempunyai komponen kecepatan sumbu-x
v = v0x = 80 m/s.
d. Waktu untuk mencapai jarak maksimum (X) diperoleh apabila y = 0 (60t – 5t2) = 0 dan diperoleh t = 12 sekon
e. Jarak mendatar maksimum tembakan
X = v0xt = 80t = (80)(12)= 96 m.
C. Gerak Melingkar
Di kelas X, Anda telah mempelajari bahwa suatu partikel dikatakan bergerak melingkar beraturan, jikalau partikel tersebut bergerak dalam lintasan berbentuk bundar atau busur bundar dengan kelajuan konstan. Walaupun kelajuan partikel tersebut tidak berubah, namun partikel tersebut tetap mempunyai percepatan. Mengapa demikian? Anda tentu telah memahami bahwa percepatan partikel (perubahan kecepatan dalam selang waktu tertentu) merupakan perubahan kelajuan partikel tersebut. Namun, Anda dihentikan lupa bahwa kecepatan merupakan besaran vektor. Oleh alasannya ialah kecepatan merupakan besaran vektor, perubahan arah kecepatan saja (besar kecepatan tetap) akan menjadikan percepatan, menyerupai yang terjadi pada gerak melingkar beraturan.
Perhatikanlah Gambar 17. berikut.
Pada gambar tersebut ditunjukkan hubungan antara vektor kecepatan dan percepatan pada gerak melingkar beraturan. Besar kecepatan dan percepatan pada gerak melingkar beraturan tidak berubah-ubah, namun arahnya selalu berubah-ubah setiap saat. Arah kecepatan selalu menyinggung lintasan bundar (tangensial terhadap lingkaran), sedangkan percepatan selalu mengarah ke sentra bundar sehingga disebut percepatan sentripetal.
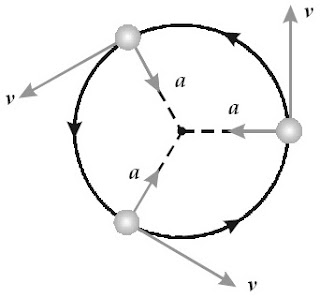 |
| Gambar 17. Arah vektor kecepatan dan percepatan pada gerak melingkar. |
Perhatikanlah Gambar 18.
Suatu partikel yang bergerak melingkar beraturan di titik P dengan jari-jari bundar r. Oleh alasannya ialah arah kecepatan selalu tegak lurus jari-jari r (tangensial terhadap lingkaran), sudut θ yang dibuat oleh v terhadap garis vertikal di titik P akan sama besar dengan sudut θ yang dibuat oleh jari-jari r terhadap sumbu-x. Vektor kecepatan di titik P tersebut sanggup diuraikan menjadi vektor komponennya berdasarkan sumbu-x dan sumbu-y, menyerupai yang ditunjukkan pada Gambar 19 berikut.
Dengan demikian, sanggup dituliskan :
 |
| Gambar 18. Partikel P bergerak melingkar berlawanan arah jarum jam. Vektor kecepatannya (v) selalu berubah-ubah terhadap waktu, walaupun besar vektor kecepatannya tetap |
 |
| Gambar 19. Kecepatan v dan komponen vektornya berdasarkan sumbu-x dan sumbu-y. |
v = vxi + vyj (1–49)
atau
v= (–v sinθ )i + (v cosθ )j (1–50)
Perhatikan kembali Gambar 18. Dari gambar tersebut, Anda dapat mengganti sinθ dengan yp r dan cosθ dengan xp/r Persamaan (1–50) sanggup ditulis menjadi :
Percepatan gerak melingkar beraturan sanggup ditentukan dari turunan pertama Persamaan (1–51) sebagai berikut.
Oleh alasannya ialah :
dan.
serta vx = -v sinθ dan vy = -v cosθ maka Persamaan (1–52) sanggup ditulis menjadi :
Vektor percepatan dan komponen vektornya berdasarkan sumbu-x dan sumbu-y ditunjukkan oleh Gambar 20.
Berdasarkan uraian gambar tersebut, sanggup ditentukan besar percepatan sentripetal melalui persamaan berikut.
 |
| Gambar 20. Percepatan a dan komponen vektornya berdasarkan sumbu-x dan sumbu-y. |
Sedangkan, arah vektor percepatan, φ , sanggup ditentukan dari persamaan :
tanφ = tanθ (1–55)
Dari Persamaan (1–54) dan Persamaan (1–55), terbukti bahwa percepatan sentripetal a = v2/r dan arahnya selalu menuju sentra bundar (φ θ = ).
Contoh Soal 15 :
Berapakah percepatan sentripetal, dalam satuan g, yang dirasakan oleh seorang pilot yang menerbangkan pesawatnya dengan kelajuan v = 2.500 km/jam dalam lintasan bundar berjari-jari r = 5,8 km?
Kunci Jawaban :
Diketahui: v = 2.500 km/jam dan r = 5,8 km.
Berdasarkan persamaan percepatan sentripetal, didapatkan :
Contoh Soal 16 :
Sebuah bola yang terikat bergerak dalam bundar horizontal yang berjari-jari 2 m. Bola menciptakan satu putaran dalam 3 s. Berapakah percepatan sentripetal bola tersebut?
Kunci Jawaban :
Diketahui: r = 2 m dan T = 3 s.
Untuk memilih percepatan sentripetal, tentukan kecepatan linear terlebih dahulu dengan cara membagi panjang lintasan dengan waktu yang dibutuhkan untuk menempuh lintasan tersebut. Dalam masalah ini panjang lintasannya berupa keliling bundar dengan jari-jari r.
v = 4,19 m/s.
Jadi, besar percepatan sentripetal bola ialah :
a = 8,78 m/s 0,9 g.
Contoh Soal 17 :
Sebuah kendaraan beroda empat mengelilingi sebuah kurva berjari-jari 30 m. Jika percepatan sentripetal maksimum yang sanggup diberikan oleh ukiran roda kendaraan beroda empat ialah 5 m/s2, berapakah kelajuan maksimum kendaraan beroda empat tersebut dalam km/jam?
Kunci Jawaban :
Diketahui: r = 30 m dan v = 5 m/s2.
vmaks = 12,2 m/s
Jadi, kelajuan maksimum kendaraan beroda empat dalam satuan km/jam ialah :
Contoh Soal 18 :
Untuk menyalurkan pinjaman kemanusiaan, sebuah pesawat kargo harus menjatuhkan kapsul besar berparasut kepada serombongan pengungsi. Jika kendala udara sebelum parasut mengembang (yakni sehabis 5 sekon dijatuhkan) diabaikan, ketinggian terbang minimal pesawat biar parasut kapsul telah mengembang di ketinggian 100 m sebelum mencapai permukaan ialah .... (g = 10 m/s2)
a. 185 m
b. 200 m
c. 215 m
d. 225 m
e 250 m
Kunci Jawaban :
Diketahui: t = 5 s, hp = 100 m, dan g = 10 m/s2.
Selisih ketinggian sebelum parasut mengembang (t = 5 s):
ht = 125 m
Ketinggian minimal pesawat:
hmin = ht + hp
hmin = 125 m + 100 m
Jawab: d
Rangkuman :
1. Persamaan gerak ialah persamaan yang menyatakan hubungan antara posisi, kecepatan, percepatan, dan waktu. Posisi suatu partikel pada sebuah bidang sanggup dinyatakan dalam bentuk vektor posisi, yaitu
r = xi + yj
2. Kecepatan ialah perubahan posisi (perpindahan) terhadap waktu sehingga sanggup ditentukan dari turunan pertama fungsi posisi terhadap waktu.
v = dr/dt
3. Percepatan merupakan perubahan kecepatan terhadap waktu sehingga sanggup ditentukan dari turunan pertama fungsi posisi, atau turunan kedua fungsi posisi terhadap waktu :
4. Gerak parabola ialah gerak adonan antara gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB)
a. Persamaan pada arah sumbu-x:
vx = v0 cosα
x = v0 cosα t
b. Persamaan pada arah sumbu-y:
vy = v0 sinα – gt
y = v0 sinα t –½ gt2
c. Waktu yang diharapkan untuk mencapai titik tertinggi :
d. Waktu yang diharapkan untuk mencapai titik terjauh :
e. Titik tertinggi yang sanggup dicapai benda :
f. Titik terjauh yang sanggup dicapai benda :
5. Gerak melingkar ialah gerak benda pada suatu lintasan yang berbentuk lingkaran.
a. Kecepatan benda yang bergerak melingkar dinyatakan dengan persamaan
v = vxi + vyj
dan besar kecepatannya dinyatakan dengan :
b. Percepatan sentripetal ialah percepatan gerak benda dikala melaksanakan gerak melingkar yang arahnya selalu menuju sentra lingkaran.
Anda kini sudah mengetahui Persamaan Gerak Benda Dua Dimensi, Gerak Parabola, Gerak Melingkar, Vektor, Kecepatan, dan Percepatan. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.
Referensi :
Saripudin, A., D. Rustiawan K., dan A. Suganda. 2009. Mudah Belajar Fisika 1 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah Program Ilmu Pengetahuan Alam. Pusat Perbukuan Departemen Nasional, Departemen Pendidikan Nasional, Jakarta. p. 234.














