Sifat Elastisas Bahan, Persamaan Gerak Harmonik, Aturan Hooke, Pegas, Gaya Pemulih, Ayunan, Periode, Frekuensi, Fase, Sudut
Sifat Elastisas Bahan, Persamaan Gerak Harmonik, Hukum Hooke, Pegas, Gaya Pemulih, Ayunan, Periode, Frekuensi, Fase, Sudut - Pada ketika Anda mengendarai motor atau mobil, pernahkah Anda mencicipi guncangan ketika motor atau kendaraan beroda empat Anda melewati lubang atau jalan yang tidak rata? Setelah kendaraan melewati lubang atau jalan yang tidak rata, kendaraan akan berguncang atau berayun beberapa kali, kemudian kendaraan Anda akan kembali berjalan dengan mulus. Tahukah Anda, mengapa insiden tersebut terjadi? Pada setiap kendaraan, terdapat sebuah sistem pegas lentur yang berkhasiat untuk memperkecil efek goncangan pada kendaraan, yaitu shockbreaker. Tahukah Anda bagaimana prinsip kerja shockbreaker tersebut? Dalam hal apa sajakah sifat lentur suatu benda diaplikasikan? Bagaimanakah korelasi antara elastisitas benda dengan gerak harmonik? Agar sanggup menjawab pertanyaan-pertanyaan tersebut, pada Bab ini akan dibahas materi perihal elastisitas benda dan gerak harmonik sederhana.
 |
| Gambar 1. Shockabsorber pada mobil. [1] |
A. Sifat Elastis Bahan
Pada Subbab A ini, Anda akan mempelajari gaya pemulih pada pegas yang memenuhi Hukum Hooke. Anda juga akan mengetahui bahwa gaya pemulih tersebut timbul akhir sifat pegas yang elastis. Bagaimana sifat lentur benda padat secara Fisika? Tahukah Anda, besaran-besaran yang memilih elastisitas suatu benda? Agar Anda sanggup menjawab pertanyaan-pertanyaan tersebut, pelajarilah bahasan materi subbab berikut dengan saksama.
1. Sifat Elastis Benda Padat
Sebuah pegas atau per kalau ditarik akan bertambah panjang. Jika ditekan, pegas atau per tersebut akan menjadi lebih pendek. Jika pegas atau per tersebut kemudian dilepaskan, pegas atau per akan kembali ke bentuknya semula. Benda yang mempunyai sifat menyerupai pegas atau per disebut benda elastis. Jika benda yang terbuat dari plastisin, lilin, atau tanah liat ditekan, sesudah gaya tekan dihilangkan, benda-benda tersebut tidak akan kembali ke bentuk semula.
Ada dua pengertian dasar dalam mempelajari sifat lentur benda padat, yaitu tegangan (stress) dan regangan (strain). Pembahasan mengenai keduanya diuraikan pada cuilan berikut.
Gambar 2a memperlihatkan suatu batang yang luasnya A. Setiap ujung batang tersebut mengalami gaya tarik sebesar F yang sama besar dan berlawanan arah. Batang itu dikatakan mengalami tegangan. Apabila ditinjau sebuah irisan tegak lurus pada panjang batang (garis putus-putus pada Gambar 2a), tarikan oleh gaya F akan tersebar rata pada luas penampang A, menyerupai ditunjukkan oleh pada Gambar 2b. Oleh alasannya itu, tegangan didefinisikan sebagai perbandingan besar gaya F terhadap luas penampang bidang A. Secara matematis dirumuskan:
dengan :
F = gaya tekan/tarik (N),
A = luas penampang yang ditekan/ditarik (m2), dan
σ = tegangan/stress (N/m2 atau pascal).
Regangan ialah perubahan relatif ukuran atau bentuk benda yang mengalami tegangan. Gambar 3.2 memperlihatkan sebuah batang yang mengalami regangan akhir gaya tarik F. Panjang batang mula-mula adalah l0. Setelah mendapat gaya tarik sebesar F, batang tersebut berubah panjangnya menjadi l . Dengan demikian, batang tersebut mendapat pertambahan panjang sebesar Δl, dengan Δl = l - l0 . Oleh alasannya itu, regangan didefinisikan sebagai perbandingan antara pertambahan panjang benda dan panjang benda mula-mula. Secara matematis dirumuskan:
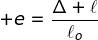 (1-2)
(1-2)
dengan :
Δ l = pertambahan panjang (m),
Δ l = pertambahan panjang (m),
lo = panjang mula-mula (m), dan
e = regangan (tidak bersatuan).
2. Modulus Elastisitas
Tegangan yang diharapkan untuk menghasilkan suatu regangan tertentu bergantung pada sifat materi dari benda yang mendapat tegangan tersebut. Menurut Hooke, perbandingan antara tegangan dan regangan suatu
benda disebut modulus Young atau modulus elastisitas benda tersebut. Secara matematis, modulus elastisitas dirumuskan sebagai berikut.
dengan satuan E dalam N/m2.
Menurut Hukum Hooke (bahasan mengenai Hukum Hooke ini akan Anda pelajari lebih rinci pada subbab B), gaya pemulih pada pegas yang berada di dalam batas elastisnya akan selalu memenuhi persamaan berikut.
F = -kD l (1-4)
dengan:
k = tetapan pegas (N/m),
k = tetapan pegas (N/m),
Δl = pertambahan panjang pegas (m), dan
F = gaya yang bekerja pada pegas (N).
Tanda minus (–) Persamaan (1–4) menyatakan arah gaya pemulih yang selalu berlawanan dengan pertambahan panjang pegas. Dari Persamaan (1–3), diperoleh :
Oleh alasannya F = kΔl, korelasi antara tetapan pegas dan modulus Young/modulus elastisitas sanggup dituliskan sebagai :
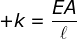
Tabel 1. Modulus Elastisitas (Harga Pendekatan)
Bahan | Modulus Young |
Aluminium | 0,7 × 1011 N/m2 |
Kuningan | 0,91 × 1011 N/m2 |
Tembaga | 1,1 × 1011 N/m2 |
Gelas | 0,55 × 1011 N/m2 |
Besi | 0,91 × 1011 N/m2 |
Timah | 0,16 × 1011 N/m2 |
Nikel | 2,1 × 1011 N/m2 |
Baja | 2 × 1011 N/m2 |
Tungsten | 3,6 × 1011 N/m2 |
Sumber: College Physics, 1983 | |
Contoh Soal 1.
Sebuah kawat logam dengan diameter 1,25 mm dan panjangnya 80 cm digantungi beban bermassa 10 kg. Ternyata kawat tersebut bertambah panjang 0,51 mm. Tentukan:
a. tegangan (stress),
b. regangan (strain), dan
c. modulus Young zat yang membentuk kawat.
Kunci Jawaban :
Contoh Soal 2.
Sebuah silinder yang terbuat dari baja panjangnya 10 m dan jari-jari 2 cm. Jika modulus elastisitas baja tersebut 2,0 × 1011 N/m2, berapakah tetapan gaya baja tersebut?
Kunci Jawaban :
B. Gerak Harmonik Sederhana
Jika suatu benda bergerak bolak-balik terhadap titik tertentu, gerak benda itu disebut bergetar. Pada subbab ini Anda akan mempelajari jenis getaran yang dinamakan gerak harmonik sederhana. Contoh gerak menyerupai ini, antara lain gerak benda yang digantungkan pada suatu pegas dan gerak ayunan bandul yang amplitudonya kecil.
Pada gerak harmonik sederhana, benda akan selalu bergerak bolak-balik di sekitar titik kesetimbangannya secara terus-menerus. Dengan demikian, definisi gerak harmonik sederhana ialah gerak bolak-balik benda melalui suatu titik kesetimbangan tertentu dengan banyaknya getaran benda dalam setiap sekon selalu konstan.
1. Gaya Pemulih
Gaya pemulih dimiliki oleh setiap benda lentur yang terkena gaya sehingga benda lentur tersebut berubah bentuk. Gaya yang timbul pada benda lentur untuk menarik kembali benda yang menempel padanya disebut gaya pemulih. Akibat gaya pemulih tersebut, benda akan melaksanakan gerak harmonik sederhana. Dengan demikian, pada benda yang melaksanakan gerak harmonik sederhana bekerja gaya pemulih yang selalu mengarah pada titik kesetimbangan benda.
a. Gaya Pemulih pada Pegas
Pegas ialah salah satu referensi benda elastis. Oleh alasannya sifat elastisnya ini, suatu pegas yang diberi gaya tekan atau gaya regang akan kembali ke keadaan setimbangnya mula-mula apabila gaya yang bekerja padanya dihilangkan. Gaya yang timbul pada pegas untuk mengembalikan posisinya ke keadaan setimbang disebut gaya pemulih pada pegas.
Gaya pemulih pada pegas banyak dimanfaatkan dalam bidang teknik dan kehidupan sehari-hari. Misalnya, pada shockbreaker kendaraan dan springbed. Di dalam shockbreaker terdapat sebuah pegas yang berfungsi meredam getaran ketika roda kendaraan melewati jalanan yang tidak rata. Dengan demikian, kendaraan sanggup dikendarai dengan nyaman. Demikian juga dengan springbed. Pegas-pegas yang tersusun di dalam springbed akan memperlihatkan kenyamanan ketika Anda tidur di atasnya. Bagaimanakah sifat-sifat gaya pemulih pada pegas ini apabila diuraikan secara Fisika? Agar Anda sanggup memahaminya, pelajarilah bahasan materi pada subbab ini.
Tokoh Fisika :
Hooke lahir di Freshwater Kepulauan Wight, Inggris. Ia banyak melaksanakan percobaan mengenai sifat lentur benda. Salah satu teorinya yang populer ialah Hukum Hooke yang menjadi dasar teori elastisitas. Ia juga populer sebagai pembuat alat/ mesin sehingga namanya diabadikan sebagai nama sebuah versi mikroskop. Bukunya yang populer ialah Micrographia. (Sumber: www.all iographies.com)
1) Hukum Hooke
Jika gaya yang bekerja pada sebuah pegas dihilangkan, pegas tersebut akan kembali ke keadaannya semula. Ilmuwan yang pertama-tama meneliti perihal ini ialah Robert Hooke. Melalui percobaannya, Hooke menyimpulkan bahwa sifat lentur pegas tersebut ada batasnya dan besar gaya pegas sebanding dengan pertambahan panjang pegas. Agar Anda sanggup memahami percobaan yang dilakukan Hooke dengan baik, lakukanlah aktivitas Mahir
Percobaan Fisika Sederhana 1.
Mengukur Pertambahan Panjang Pegas
Alat dan Bahan :
- Satu pegas dengan jarum penunjuk di ujungnya
- Lima beban masing-masing 50 gram
- Statif
- Penggantung beban
- Penggaris atau skala pengukur
- Susunlah alat-alat percobaan menyerupai pada gambar.
- Catatlah skala yang ditunjukkan oleh jarum penunjuk ketika pegas digantung tanpa beban.
- Gantungkanlah beban 1 pada pegas, kemudian catat skala yang ditunjukkan oleh jarum penunjuk.
- Ulangi langkah ke-3 dengan menambahkan beban 2, beban 3, beban 4, dan beban 5.
- Tuliskanlah hasil pencatatan skala yang ditunjukkan oleh jarum penunjuk ke dalam tabel.
- Kurangilah beban dari pegas satu per satu, kemudian tuliskan nilai skala yang ditunjukkan oleh jarum penunjuk ke dalam tabel.
- Hitunglah skala penunjukan rata-rata untuk setiap berat beban dan pertambahan panjang pegas yang dihasilkannya.
- Plot grafik pertambahan panjang pegas terhadap berat beban.
- Diskusikan hasil percobaan Anda kemudian laporkan kepada guru.
Berat Beban (gram) | Penambahan Skala (cm) | Pembacaan Skala Rata-Rata | Pertambahan Panjang Pegas (cm) | |
Penambahan Beban | Pengurangan Beban | |||
Dari percobaan tersebut, Anda sanggup menyimpulkan bahwa suatu pegas apabila ditarik dengan gaya tertentu di kawasan yang berada dalam batas kelentingannya akan bertambah panjang sebesar Δx. Dari hasil percobaan, juga didapatkan bahwa besar gaya pegas pemulih sebanding dengan pertambahan panjang pegas (Δx). Secara matematis, pernyataan tersebut sanggup dituliskan sebagai berikut.
F = -kΔx (1-6)
dengan k = tetapan pegas (N/m).
Persamaan (1–6) ini dikenal sebagai Hukum Hooke. Tanda negatif (–) diberikan alasannya arah gaya pemulih pada pegas selalu berlawanan dengan arah gerak pegas tersebut. Perhatikanlah grafik korelasi antara F dan Δx pada Gambar 4.
Dari titik O hingga dengan titik P, grafik F–Δx berbentuk garis lurus. Dalam batasan ini, pertambahan panjang pegas linear dan titik P disebut sebagai batas linearitas pegas. Dari titik P hingga dengan titik Q, pertambahan panjang pegas tidak linear sehingga F tidak sebanding dengan Δx. Namun hingga titik Q ini pegas masih bersifat elastis. Di atas batas lentur ini terdapat kawasan tidak lentur (plastis). Pada kawasan ini, pegas sanggup putus atau tidak kembali ke bentuknya semula, walaupun gaya yang bekerja pada pegas itu dihilangkan. Hukum Hooke hanya berlaku hingga batas linearitas pegas.
 |
| Gambar 4. Grafik korelasi antara gaya dan pertambahan penjang pegas. |
Dari grafik F– Δx pada Gambar 4. juga sanggup ditentukan tetapan pegas (k) pada batas linearitas pegas, yaitu:
k = F/Δx = tan α = kemiringan grafik F(-Δx) (1-7)
Contoh Soal 3.
Benda bermassa 4,5 kg digantungkan pada pegas sehingga pegas itu bertambah panjang sebesar 9 cm. Berapakah tetapan pegas tersebut?
Kunci Jawaban :
Diketahui: m = 4,5 kg, g = 10 m/m2, dan Δx = 9 cm.
F = k Δx
mg = k Δx
(4,5 kg)(10 m/s2) = (k)(0,09 m)
k = (45kg / 0,09 m) = 500 N/m
k = (45kg / 0,09 m) = 500 N/m
Contoh Soal 4.
Sebuah pegas yang digantungkan vertikal panjangnya 10 cm. Jika pegas diberi beban 1,2 kg, pegas akan bertambah panjang menjadi 19 cm. Berapakah panjang pegas tersebut kalau diberi beban 1 kg?
Kunci Jawaban :
Diketahui: x1 = 10 cm, m1 = 1,2 kg, x2 = 19 kg, dan m2 = 1 kg.
mg = k Δx → m ≈ Δx
Massa beban (m) berbanding lurus dengan pertambahan panjang (Δx) sehingga diperoleh persamaan :
x = 17,5 cm.
2) Susunan Pegas
Konstanta pegas sanggup berubah nilainya, apabila pegas-pegas tersebut disusun menjadi rangkaian. Hal ini diperlukan, kalau Anda ingin mendapat suatu nilai konstanta pegas untuk tujuan mudah tertentu, contohnya dalam merancang pegas yang dipakai sebagai shockbreaker. Besar konstanta total rangkaian pegas bergantung pada jenis rangkaian pegas, yaitu rangkaian pegas seri atau rangkaian pegas paralel.
Perhatikanlah Gambar 5. Gaya yang bekerja pada setiap pegas ialah sebesar F. Dengan demikian, setiap pegas akan mengalami pertambahan panjang sebesar Δx1 dan Δx2. Pertambahan panjang total kedua pegas adalah Δxtotal = Δx1 dan Δx2. Menurut Hukum Hooke, konstanta pegas total rangkaian pegas yang di susun seri tersebut ialah :
dengan kn = konstanta pegas ke-n.
Gambar 6. memperlihatkan dua pegas yang dirangkai secara paralel. Jika rangkaian pegas itu ditarik dengan gaya sebesar F, setiap pegas akan mengalami gaya tarik sebesar F1 dan F2 dengan Ftotal = F1 + F2 Setiap pegas juga akan mendapat pertambahan panjang sebesar Δx1 dan Δx2. Oleh alasannya Δx1 dan Δx2, konstanta pegas total untuk rangkaian pegas paralel berdasarkan Hukum Hooke ialah :
Secara umum, konstanta total pegas yang dirangkai paralel dinyatakan dengan persamaan :
ktotal = k1 + k2 + k3 + ... + kn (1-11)
ktotal = k1 + k2 + k3 + ... + kn (1-11)
dengan kn = konstanta pegas ke-n.
Contoh Soal 5.
Dua pegas identik mempunyai tetapan pegas 600 N/m. Tentukanlah konstanta sistem pegas jika:
a. disusun seri
b. disusun paralel
Kunci Jawaban :
Contoh Soal 6.
Perhatikanlah gambar sistem pegas di bawah ini.
Jika k1 = k2 = 600 N/m, k3 = 1.200 N/m, dan m = 3 kg, tentukanlah:
Jika k1 = k2 = 600 N/m, k3 = 1.200 N/m, dan m = 3 kg, tentukanlah:
a. tetapan sistem pegas, dan
b. pertambahan panjang sistem pegas.
Kunci Jawaban :
Perhatikanlah ilustrasi gerakan pegas dan gaya pemulihnya yang diperlihatkan pada Gambar 7.
Gambar tersebut memperlihatkan suatu pegas yang konstanta pegasnya k dan panjangnya ketika belum digantungi beban adalah l. Setelah benda bermassa m digantungkan pada pegas, menyerupai pada Gambar 7b, pegas bertambah panjang sebesar Δl dan berada dalam keadaan setimbang. Gaya pemulih yang timbul pada pegas sama dengan berat benda, mg. Apabila pegas yang digantungi beban itu ditarik ke bawah dengan gaya sebesar F, pegas bertambah panjang sebesar Δl2, menyerupai terlihat pada Gambar 7c.
Pada ketika ini, gaya pemulih pada pegas memenuhi korelasi sesuai Hukum Hooke F = –kΔl dengan Δl = Δl2.
Contoh Soal 7.
Pegas yang tergantung tanpa beban panjangnya 25 cm. Kemudian, ujung bawah pegas digantungi beban 100 gram sehingga panjang pegas menjadi 30 cm. Jika beban ditarik ke bawah sejauh 4 cm dan percepatan gravitasi Bumi 10 m/s2, tentukan gaya pemulih pada pegas itu.
Kunci Jawaban :
Perhatikanlah gambar.
Diketahui: y = 25 cm, y1 = 30 cm, y2 = 4 cm, m = 100 g, dan g = 10 m/s2.
Pada posisi gambar (b) :
mg = ky1
(0,1 kg)(10 m/s) = k(0,05 m)
k = 20 N/m
Pada posisi gambar (c) :
F = ky2 = (20 N/m) (0,04 m) = 0,8 N
b. Gaya Pemulih pada Ayunan Matematis
Ayunan matematis atau ayunan sederhana merupakan suatu partikel massa yang tergantung pada suatu titik tetap pada seutas tali, di mana massa tali sanggup diabaikan dan tali tidak sanggup bertambah panjang. Contoh ayunan matematis ini ialah jam bandul.
Perhatikanlah Gambar 8a. Sebuah beban bermassa m tergantung pada seutas kawat halus kaku sepanjang l dan massanya sanggup diabaikan. Apabila bandul itu bergerak vertikal dengan membentuk sudut θ, menyerupai terlihat pada Gambar 8b, gaya pemulih bandul tersebut ialah mg sin θ. Secara matematis sanggup dituliskan :
F = – mg sinθ (1-12)
Oleh alasannya :
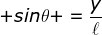
Persamaan (3–12) sanggup dituliskan sebagai berikut.
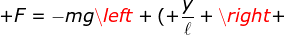)
 |
| Gambar 8. (a) Sebuah bandul digantungkan pada kawat halus sepanjang l . (b) Kemudian, bandul disimpangkan sejauhθ sehingga gaya pemulih bandul ialah F = -mg sinθ = -mg (y/l) |
Sebuah ayunan sederhana mempunyai panjang tali = 40 cm dengan beban = 100 gram. Tentukanlah besar gaya pemulihnya kalau benda disimpangkan sejauh 4 cm dan percepatan gravitasi di tempat itu = 10 m/s2.
Kunci Jawaban :
Contoh Soal 9.
Sebuah ayunan sederhana mempunyai panjang tali 30 cm dengan beban 200 gram. Berapa jauh benda harus disimpangkan biar besar gaya pemulihnya 0,4 N?
Kunci Jawaban :
Diketahui: l = 30 cm, m = 200 g, dan F = 0,4 N.
2. Persamaan Gerak Harmonik Sederhana
a. Persamaan Simpangan Gerak Harmonik Sederhana
Persamaan gerak harmonik sederhana didapatkan dari proyeksi gerak melingkar beraturan pada sumbu-x atau sumbu-y. Perhatikanlah Gambar 9 yang memperlihatkan sebuah kereta mainan sedang bergerak melingkar di jalurnya.
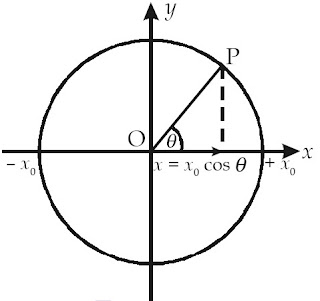 |
| Gambar 10. Proyeksi titik P yang bergerak melingkar beraturan pada sumbu-x ialah x0 cosθ . |
x = x0 cosθ (1-13)
Di kelas X, Anda telah mempelajari bahwa periode (T) ialah waktu yang dibutuhkan untuk melaksanakan satu putaran penuh. Oleh alasannya θ= 2π maka waktu yang dibutuhkan oleh titik P untuk bergerak dari titik +x0 hingga ke posisinya digambar ialah :
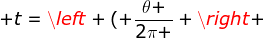T) (1-14)
(1-14)
Dengan demikian, korelasi antara sudut dan waktu sanggup juga dituliskan sebagai :
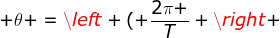t) (1-15)
(1-15)
Apabila Persamaan (1–15) disubstitusikan ke Persamaan (1–14) didapatkan :
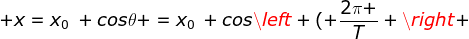t) (1-16)
(1-16)
Anda telah mengetahui bahwa frekuensi berbanding terbalik dengan periode
Anda telah mengetahui bahwa frekuensi berbanding terbalik dengan periode :
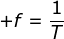
Dengan demikian, Persamaan (1–16) sanggup ditulis sebagai :
x = x0 cos 2πft (1-17)
Oleh alasannya :
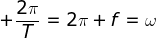
ω (kecepatan sudut), Persamaan (1–16) dan Persamaan (1–17) sanggup dituliskan :
x = x0 cosω t (1-18)
dengan:
x = simpangan getaran benda (m),
x0 = jari-jari bundar atau amplitudo atau simpangan terjauh getaran benda (m),
ω = kecepatan sudut (rad/s), dan
t = waktu getar (sekon).
Persamaan-persamaan yang telah diuraikan, yaitu Persamaan (1–13) hingga Persamaan (1–18) menyatakan gerak melingkar benda yang diproyeksikan terhadap sumbu-x. Apabila gerak melingkar benda diproyeksikan berdasarkan sumbu-y, persamaan posisi benda dinyatakan sebagai y = y0 sinθ sehingga diperoleh persamaan simpangan gerak harmonik sederhana :
y = y0 sinω t (1-19)
Gambar 11. memperlihatkan korelasi antara simpangan (y) terhadap waktu (t) dari persamaan simpangan y = A sin ω t. Dari grafik tersebut sanggup diketahui bahwa nilai simpangan (ymaks) = A, yaitu amplitudo simpangan tersebut.
b. Persamaan Kecepatan Gerak Harmonik
Anda telah mempelajari bahwa kecepatan ialah adalah turunan pertama dari fungsi posisi. Hal ini juga dalam gerak harmonik. Kecepatan gerak harmonik. Secara matematis, dituliskan sebagai berikut :
dengan:
A = amplitudo/simpangan maksimum getaran (m),
ω = kecepatan sudut (rad/s), dan
t = waktu getar (sekon).
Apabila persamaan simpangan gerak harmonik dinyatakan dalam arah sumbu-x, persamaan kecepatan gerak harmoniknya ialah :
Nilai kecepatan maksimum untuk Persamaan (1–20) dan (1–21) diperoleh ketika nilai cosω t atau sinω t = 1 sehingga didapatkan nilai kecepatan maksimum gerak harmonik ialah :
vmaks = Aω (1-22)
Oleh karena sin2 ωt + cos2 ωt = 1 dan A2 cos2 ωt = A2 – A2 sin2 ωt, kecepatan getar sanggup juga dihitung dengan rumus lain, yaitu :
c. Persamaan Percepatan Gerak Harmonik
Persamaan percepatan gerak harmonik sanggup ditentukan dari turunan pertama persamaan kecepatan gerak harmonik terhadap waktu. Secara matematis, penulisannya ialah sebagai berikut.
Oleh alasannya A sinω t = y, persamaan percepatan gerak harmonik sanggup dituliskan menjadi :
a = –ω2y (1-25)
Nilai percepatan maksimum untuk Persamaan (1–24) diperoleh ketika sinω t = 1 sehingga nilai percepatan maksimum gerak harmonik dinyatakan sebagai :
amaks = –Aω2 (1-26)
Tanda negatif (–) pada persamaan percepatan gerak harmonik memperlihatkan bahwa arah percepatan gerak selalu menuju ke titik kesetimbangannya, yaitu y = 0.
Catatan Fisika :
Pegas dan fluida kental yang terdapat pada shock breaker kendaraan mengakibatkan efek redaman terhadap gerak harmonik yang terjadi ketika kendaraan berguncang. Redaman ini dibutuhkan biar kendaraan tidak berosilasi selamanya.
Contoh Soal 10.
Sebuah titik materi melaksanakan gerak harmonik dengan amplitudo 5 cm. Berapakah simpangannya pada ketika sudutnya 30°?
Kunci Jawaban :
Diketahui: A = 5 cm dan θ = 30°.
Dengan demikian, Persamaan (1–16) sanggup ditulis sebagai :
x = x0 cos 2πft (1-17)
Oleh alasannya :
ω (kecepatan sudut), Persamaan (1–16) dan Persamaan (1–17) sanggup dituliskan :
x = x0 cosω t (1-18)
dengan:
x = simpangan getaran benda (m),
x0 = jari-jari bundar atau amplitudo atau simpangan terjauh getaran benda (m),
ω = kecepatan sudut (rad/s), dan
t = waktu getar (sekon).
Persamaan-persamaan yang telah diuraikan, yaitu Persamaan (1–13) hingga Persamaan (1–18) menyatakan gerak melingkar benda yang diproyeksikan terhadap sumbu-x. Apabila gerak melingkar benda diproyeksikan berdasarkan sumbu-y, persamaan posisi benda dinyatakan sebagai y = y0 sinθ sehingga diperoleh persamaan simpangan gerak harmonik sederhana :
y = y0 sinω t (1-19)
Gambar 11. memperlihatkan korelasi antara simpangan (y) terhadap waktu (t) dari persamaan simpangan y = A sin ω t. Dari grafik tersebut sanggup diketahui bahwa nilai simpangan (ymaks) = A, yaitu amplitudo simpangan tersebut.
 |
| Gambar 11. Proyeksi titik P terhadap sumbu-y ialah y = y0 sinθ. |
Anda telah mempelajari bahwa kecepatan ialah adalah turunan pertama dari fungsi posisi. Hal ini juga dalam gerak harmonik. Kecepatan gerak harmonik. Secara matematis, dituliskan sebagai berikut :
dengan:
A = amplitudo/simpangan maksimum getaran (m),
ω = kecepatan sudut (rad/s), dan
t = waktu getar (sekon).
Apabila persamaan simpangan gerak harmonik dinyatakan dalam arah sumbu-x, persamaan kecepatan gerak harmoniknya ialah :
Nilai kecepatan maksimum untuk Persamaan (1–20) dan (1–21) diperoleh ketika nilai cosω t atau sinω t = 1 sehingga didapatkan nilai kecepatan maksimum gerak harmonik ialah :
vmaks = Aω (1-22)
Oleh karena sin2 ωt + cos2 ωt = 1 dan A2 cos2 ωt = A2 – A2 sin2 ωt, kecepatan getar sanggup juga dihitung dengan rumus lain, yaitu :
c. Persamaan Percepatan Gerak Harmonik
Persamaan percepatan gerak harmonik sanggup ditentukan dari turunan pertama persamaan kecepatan gerak harmonik terhadap waktu. Secara matematis, penulisannya ialah sebagai berikut.
Oleh alasannya A sinω t = y, persamaan percepatan gerak harmonik sanggup dituliskan menjadi :
a = –ω2y (1-25)
Nilai percepatan maksimum untuk Persamaan (1–24) diperoleh ketika sinω t = 1 sehingga nilai percepatan maksimum gerak harmonik dinyatakan sebagai :
amaks = –Aω2 (1-26)
Tanda negatif (–) pada persamaan percepatan gerak harmonik memperlihatkan bahwa arah percepatan gerak selalu menuju ke titik kesetimbangannya, yaitu y = 0.
Catatan Fisika :
Shockbreaker
Pegas dan fluida kental yang terdapat pada shock breaker kendaraan mengakibatkan efek redaman terhadap gerak harmonik yang terjadi ketika kendaraan berguncang. Redaman ini dibutuhkan biar kendaraan tidak berosilasi selamanya.
Contoh Soal 10.
Sebuah titik materi melaksanakan gerak harmonik dengan amplitudo 5 cm. Berapakah simpangannya pada ketika sudutnya 30°?
Kunci Jawaban :
Diketahui: A = 5 cm dan θ = 30°.
y = A sinω t = 5 sin 30° = (5 cm) (1/2) = 2,5 cm.
Contoh Soal 11 :
Sebuah benda bermassa 2 gram digetarkan berdasarkan persamaan y = 0,05 sin 300t (semua satuan dalam SI). Tentukan kecepatan dan percepatan benda pada ketika t = 0,6 s.
Kunci Jawaban :
Diketahui: m = 2 g, y = 0,05 sin 300t, dan t = 0,6 s.
Contoh Soal 12 :
Sebuah partikel bergetar harmonik dengan periode 5 sekon dan amplitudo 7,5 cm. Berapakah kelajuan partikel pada ketika berada 4,5 cm dari titik setimbangnya?
Kunci Jawaban :
Diketahui: T = 5 sekon, A = 7,5 cm, dan y = 4,5 cm.
Contoh Soal 13 :
Sebuah titik melaksanakan gerak harmonik sederhana dengan periode T = 60 ms. Berapakah waktu minimum yang diharapkan titik biar simpangannya sama dengan setengah amplitudonya?
Kunci Jawaban :
Diketahui T = 60 ms.
Gunakan persamaan simpangan untuk memilih waktu t biar y = 1/2 A.
Sebuah benda bermassa 2 gram digetarkan berdasarkan persamaan y = 0,05 sin 300t (semua satuan dalam SI). Tentukan kecepatan dan percepatan benda pada ketika t = 0,6 s.
Kunci Jawaban :
Diketahui: m = 2 g, y = 0,05 sin 300t, dan t = 0,6 s.
Contoh Soal 12 :
Sebuah partikel bergetar harmonik dengan periode 5 sekon dan amplitudo 7,5 cm. Berapakah kelajuan partikel pada ketika berada 4,5 cm dari titik setimbangnya?
Kunci Jawaban :
Diketahui: T = 5 sekon, A = 7,5 cm, dan y = 4,5 cm.
Contoh Soal 13 :
Sebuah titik melaksanakan gerak harmonik sederhana dengan periode T = 60 ms. Berapakah waktu minimum yang diharapkan titik biar simpangannya sama dengan setengah amplitudonya?
Kunci Jawaban :
Diketahui T = 60 ms.
Gunakan persamaan simpangan untuk memilih waktu t biar y = 1/2 A.
Contoh Soal 14 :
Sebuah gerak harmonik sederhana mempunyai amplitudo A = 6 cm. Berapakah simpangan getarnya ketika kecepatannya 1/2 kali kecepatan maksimum?
Kunci Jawaban :
Catatan Fisika :
Jam Pendulum
Pendulum yang terdapat pada jam merupakan salah satu referensi gerak harmonik. Ayunan matematis pendulum tersebut berfungsi untuk mengatur gerak jarum jam. Anda pun sanggup merancang jam pendulum Anda sendiri dengan memanfaatkan bahan-bahan yang terdapat di sekitar lingkungan Anda dan memahami konsep gerak harmonik sederhana ini.
3. Fase dan Sudut Fase Gerak Harmonik Sederhana
Pada persamaan gerak harmonik sederhana dikenal beberapa istilah, menyerupai fase dan sudut fase. Secara fisis, fase ialah kedudukan suatu benda dilihat dari arah getar dan simpangannya pada suatu ketika tertentu. Secara matematis, pernyataan ini dituliskan :
 |
| Gambar 12. Sebuah gelombang sinus dengan simpul-simpulnya pada titik A, C, E, G, dan I, serta titik-titik puncaknya pada titik B, D, F, dan H. |
Δθ = n. 2 π ; n = 0, 1, 2, ... atau
Δϕ = n ; n = 0, 1, 2, ...
Titik A dan titik C, titik B dan titik D dikatakan berlawanan fase alasannya arah getarnya berlawanan. Syarat biar dua titik mempunyai fase yang berlawanan ialah :
Δθ = (2n + 1) π ; n = 0, 1, 2, ... atau
Δϕ = (2n + 1) ; n = 0, 1, 2, ...
Apabila fase dan sudut fase getaran gerak harmonik diperhitungkan, akan didapatkan sebuah persamaan umum gerak harmonik sederhana yang dituliskan sebagai berikut.
y = A sin (ωt + θ0) (1-28)
dengan θ 0 = sudut fase awal getaraan (rad). Oleh alasannya itu, dari Persamaan (3–28) sanggup dinyatakan sudut fase :
Contoh Soal 15 :
Dua buah titik partikel melaksanakan gerak harmonik sederhana pada satu garis lurus. Kedua titik partikel awalnya bergerak dari titik kesetimbangan pada ketika dan arah yang sama. Periode masing-masing titik partikel adalah T1 = 1/3 sekon dan T2 = 1/4 sekon. Tentukan:
a. sudut fase θ1 dan θ2,
b. fase ϕ1 dan ϕ2, dan
c. beda fase Δϕ kedua titik partikel sesudah bergerak selama t = 1/12 sekon.
Jawab :
4. Periode dan Frekuensi Gerak Harmonik Sederhana
Setiap benda yang melaksanakan gerak harmonik sederhana mempunyai besaran periode dan frekuensi. Berikut akan dibahas periode dan frekuensi pada getaran pegas dan ayunan sederhana.
a. Periode dan Frekuensi pada Getaran Pegas
 |
| Gambar 13. Suatu pegas melaksanakan gerak harmonik di sekitar titik setimbangnya |
Periode dan frekuensi getaran pegas diperoleh dari persamaan gaya pemulih dan Hukum Kedua Newton perihal gerak, yaitu :
F = –ky = ma
Oleh alasannya pada gerak harmonik y = A sinω t dan a = –ω2y, persamaan dituiskan menjadi
–kA sinω t = m( –ω2y)
k = mω2 = m (2πf )2
sehingga diperoleh persamaan :
dengan:
m = massa beban pegas (kg), dan
k = konstanta pegas (N/m).
Contoh Soal 16 :
Sebuah pegas yang panjangnya 16 cm digantungkan vertikal. Kemudian, ujung bawahnya diberi beban 100 gram sehingga panjangnya bertambah 4 cm. Beban ditarik 3 cm ke bawah, kemudian dilepas hingga beban bergetar harmonik. Jika g = 10 m/s2,. tentukan:
a. tetapan pegas, dan
b. periode dan frekuensi getarannya.
Kunci Jawaban :
Diketahui: l = 16 cm, m = 100 g, dan y = 4 cm.
b. Periode dan Frekuensi pada Ayunan Sederhana
Periode ayunan ialah waktu yang dibutuhkan ayunan itu untuk melaksanakan satu kali gerak bolak-balik dari titik P – O – Q – O – P, menyerupai terlihat pada Gambar 14.
 |
| Gambar 14. Ayunan bandul sederhana yang bergetar harmonik di sekitar titik kesetimbangannya. |
sehingga diperoleh persamaan periode dan frekuensi pada ayunan sederhana sebagai berikut.
dengan :
l = panjang tali (m), dan
g = percepatan gravitasi (m/s2).
Contoh 17 :
Sebuah ayunan sederhana melaksanakan gerak harmonik sederhana dengan panjang tali 40 cm. Jika g = 10 m/s2, tentukanlah periode dan frekuensi ayunan tersebut.
Kunci Jawaban :
Diketahui : l = 40 cm dan g = 10 m/s2.
Contoh Soal 18 :
Beban 100 gram digantungkan pada sebuah ayunan sederhana, kemudian disimpangkan sehingga bergerak bolak-balik dengan frekuensi 5 Hz. Jika panjang tali ayunan tersebut dikurangi sebesar 3/4-nya, tentukanlah frekuensinya.
Kunci Jawaban :
Diketahui: m = 100 g, f = 5 Hz, dan l2 = 3/4 l1 .
Hubungan frekuensi dan panjang tali dirumuskan :
Contoh Soal 19.
Sebuah ayunan sederhana menciptakan 30 ayunan dalam 1 menit. Jika g = 10 m/s2 dan π2 = 10, berapakah panjang tali ayunan tersebut?
Kunci Jawaban :
Diketahui: banyak ayunan = 30, t = 1 menit, g = 10 m/s2, dan π2 = 10.
Frekuensi ayunan ialah banyaknya ayunan setiap sekon sehingga :
f = (30 ayunan / 60detik) = 1/2 Hz
Frekuensi ayunan untuk memilih panjang tali l adalah :
sehingga :
Contoh Soal 20 :
Pada getaran harmonik, kalau massa beban yang digantung pada ujung bawah pegas 1 kg, periode getarannya 2 sekon. Jika massa beban ditambah menjadi 4 kg, periode getaran menjadi ....
a. 1/4 sekon
b. 1/2 sekon
c. 1 sekon
d. 4 sekon
e. 8 sekon
Kunci Jawaban :
Getaran harmonik pada pegas :
Anda kini sudah mengetahui Sifat Elastisas Bahan dan Persamaan Gerak Harmonik dan Hukum Hooke. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.
Referensi :
Saripudin, A., D. Rustiawan K., dan A. Suganda. 2009. Mudah Belajar Fisika 1 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah Program Ilmu Pengetahuan Alam. Pusat Perbukuan Departemen Nasional, Departemen Pendidikan Nasional, Jakarta. p. 234.
Referensi Lainnya :
[1] http://en.wikipedia.org/wiki/Shock_absorber
[2] http://id.wikipedia.org/wiki/Robert_Hooke
Hewitt, Paul G. 1998. Conceptual Physics, Eight Edition. New York: Addison Wesley Longman.
Referensi Lainnya :
[1] http://en.wikipedia.org/wiki/Shock_absorber
[2] http://id.wikipedia.org/wiki/Robert_Hooke
Hewitt, Paul G. 1998. Conceptual Physics, Eight Edition. New York: Addison Wesley Longman.



































