Cara Cepat Melukiskan Vektor Resultan Dengan Metode Grafis

Dalam artikel wacana sifat-sifat vektor, telah disebutkan bahwa terdapat lima macam sifat vektor dan salah satunya yaitu vektor sanggup dijumlahkan atau dikurangkan. Lalu apa hubungannya antara kedua sifat vektor tersebut dengan resultan vektor? Resultan vektor yaitu hasil penjumlahan atau pengurangan beberapa vektor. Bisa dua vektor atau lebih.

Untuk memilih resultan vektor terdapat 2 metode yang digunakan, yaitu metode grafis dan metode analisis. Menentukan resultan dengan memakai metode grafis yaitu dengan cara melukis dua vektor atau lebih menurut besar dan arahnya membentuk suatu bidang datar. Sedangkan metode analisis yaitu cara memilih resultan vektor melalui proses penguraian vektor.

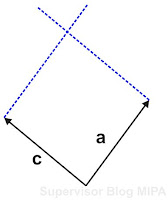
Dalam artikel ini akan dibahas wacana cara memilih resultan vektor dengan metode grafis. Sementara itu metode grafis ini sendiri terdapat tiga macam, yaitu metode segitiga, metode jajargenjang dan metode poligon. Berikut ini akan dibahas satu per satu secara tuntas. Untuk memilih resultan memakai tiga metode tersebut, perhatikan gambar empat buah vektor ini sebagai contoh untuk memilih vektor resultannya.

Gambar Vektor Acuan

Cara Melukiskan Resultan Vektor dengan Metode Segitiga

#1 Penjumlahan Vektor dengan Metode Segitiga

Jika diketahui vektor a, b, c dan d seperti pada Gambar Acuan Vektor di atas, gambarkan hasil penjumlahan a + c! untuk menggambarkan hasil penjumlahan a + c, ikuti langkah-langkah berikut: 
1. Gambarlah vektor a

2.Gambarlah vektor c dengan titik tangkap atau titik pangkalnya berada di ujung vektor a

3.Gambarlah sebuah vektor dimulai dari titik tangkap vektor a menuju ujung vektor c. Vektor ini merupakan vektor hasil penjumlahan a + c atau disebut resultan vektor yang dilambangkan R.

#2 Pengurangan/Selisih Vektor dengan Metode Segitiga

Jika diketahui vektor a, b, c dan d seperti pada Gambar Acuan Vektor di atas, gambarkan hasil pengurangan atau selisih  a − c! untuk menggambarkan hasil pengurangan a − c, ikuti langkah-langkah berikut: 
1. Gambarlah vektor a

2.Gambarlah vektor c dengan titik tangkap atau titik pangkalnya berada di ujung vektor a. Kemudian putar 180o (searah jarum jam) vektor c tersebut dari arah semula. Hal ini dilakukan alasannya yaitu pada dasarnya a − c = a + (−c), karena vektor −c sama dengan vektor c tetapi dengan arah yang berlawanan.

3.Gambarlah sebuah vektor dimulai dari titik tangkap vektor a menuju ujung vektor −c. Vektor ini merupakan resultan  dari pengurangan a – c.

Itu tadi cara cepat melukiskan resultan vektor memakai metode segitiga. Pada metode segitiga ini, kita hanya sanggup memilih resultan dari 2 vektor saja, sehingga kalau lebih dari 2 vektor, kita tidak sanggup memilih resultannya dengan metode segitiga. Metode yang sanggup dipakai yaitu metode jajargenjang dan poligon.

Cara Melukiskan Resultan Vektor dengan Metode Jajargenjang

#1 Penjumlahan Vektor dengan Metode Jajargenjang

Sekarang kita akan mencoba untuk menggambarkan penjumlahan vektor a + c dengan metode jajarangenjang. Coba kalian lihat kembali Gambar Vektor Acuan di atas. Untuk menggambarkan resultan a + c dengan metode jajargenjang, ikuti langkah-langkah berikut ini: 
1. Gambarlah vektor a

2.Gambarlah vektor c dengan titik tangkap sempurna berada pada titik tangkap vektor a

3.Buatlah garis yang sejajar dengan vektor a yang dimulai dari ujung vektor c. kemudian buat lagi garis yang sejajar dengan vektor c yang dimulai dari ujung vektor a sehingga 2 vektor dan 2 garis sejajar tersebut membentuk berdiri jajargenjang.

4.Buatlah sebuah garis vektor yang dimulai dari titik tangkap kedua vektor (a dan c) dan berakhir diperpotongan 2 garis yang sejajar tadi ibarat pada langkah 3. Vektor ini merupakan resultan dari penjumlahan a + c.

#2 Pengurangan/Selisih Vektor dengan Metode Jajargenjang

Cara mengurangkan vektor dengan metode jajar genjang bahwasanya sama saja dengan cara mengurangkan vektor dengan metode segitiga. Yang membedakan hanya letak resultan vektornya saja. Untuk menggambarkan resultan a − c dengan metode jajargenjang, ikuti langkah-langkah berikut ini: 
1. Gambarlah vektor a

2.Gambarlah vektor c dengan titik tangkap sempurna berada pada titik tangkap vektor a. Kemudian putar −180o (berlawanan arah jarum jam) vektor c tersebut dari arah semula. Sehingga menghasilkan vektor –c.

3.Buatlah garis yang sejajar dengan vektor a yang dimulai dari ujung vektor –c. kemudian garis yang sejajar dengan vektor –c yang dimulai dari ujung vektor a sehingga membentuk jajargenjang.

4.Buatlah sebuah vektor yang dimulai dari titik tangkap kedua vektor (a dan –c) dan berakhir diperpotongan 2 garis yang sejajar tadi ibarat pada langkah 3. Vektor ini merupakan resultan dari selisih a – c.

Itu tadi cara memilih resultan vektor dengan memakai metode jajargenjang. Pada artikel ini hanya membahas cara melukiskan resultan dari 2 vektor saja memakai metode ini. Untuk melukiskan resultan lebih dari 2 vektor silahkan baca artikel wacana cara melukiskan resultan 5 vektor dengan metode jajargenjang.

Cara Melukiskan Resultan Vektor dengan Metode Poligon

#1 Penjumlahan Vektor dengan Metode Poligon

Pada dasarnya, menggambarkan penjumlahan vektor dengan metode poligon sama dengan metode segitiga. Metode segitiga hanya sanggup dipakai untuk menjumlahkan 2 vektor saja, sedangkan metode poligon dipakai untuk menjumlahkan lebih dari 2 vektor.

Perhatikan kembali Gambar Vektor Acuan di atas. Sekarang kita akan mencoba menggambarkan resultan penjumlahan dari a + c + b + d dengan metode poligon. Untuk itu, perhatikan langkah-langkah berikut. 
1. Gambarlah vektor a.

2.Gambarlah vektor c dengan titik tangkap atau pangkalnya berada di ujung vektor a.

3.Gambarlah vektor b dengan titik tangkap atau pangkalnya berada di ujung vektor c.

4.Gambarlah vektor d dengan titik tangkap atau pangkalnya berada di ujung vektor b.

5.Gambarlah sebuah vektor yang dimulai dari titik tangkap atau pangkal vektor a dan berakhir di ujung vektor d. Vektor ini merupakan resultan dari penjumlahan vektor a + c + b + d.

#2 Pengurangan/Selisih Vektor dengan Metode Poligon

Untuk pengurangan vektor memakai metode poligon caranya sama persis dengan pengurangan vektor memakai metode segitiga. Kita hanya perlu membalik arah salah satu atau lebih vektor 180o (searah jarum jam) atau −180o (berlawanan arah jarum jam), sehingga tidak perlu dijelaskan tahapan demi tahapannya.

Gambar berikut ini yaitu contoh pengurangan/selisih vektor memakai metode poligon yang menghasilkan resultan a + c – b – d.

Coba kalian cermati hasil selesai dari penjumlahan dan pengurangan resultan dengan metode poligon tersebut. Kenapa resultan a + c + b + d lebih kecil dari resultan a + c – b – d? alasannya yaitu intinya selisih vektor yaitu penjumlahan vektor dengan arah yang berlawanan. Kaprikornus tanda minus (−) pada vektor bukan mengatakan nilai tetapi mengatakan arahnya sehingga tidak menghipnotis besar kecilnya resultan vektor.

Demikianlah artikel wacana cara cepat melukiskan resultan vektor dengan metode segitiga, jajargenjang dan poligon. Semoga sanggup bermanfaat untuk Anda. Terimakasih atas kunjungannya dan hingga jumpa di artikel berikutnya.

Share this post