Menentukan Rumus Koefisien Gesek Benda Di Bidang Miring, Pola Soal Dan Pembahasan
Tentunya kalian telah mengetahui bahwa besar kecilnya gaya gesek sangat dipengaruhi oleh tingkat kekasaran permukaan benda dan bidang yang bersentuhan. Tingkat kekasaran ini dinyatakan dengan koefisien gesekan. Ada dua jenis koefisien gesek, yaitu koefisien gesek statis yang dilambangkan dengan μs dan koefisien gesek kinetis yang dilambangkan dengan μk.
Koefisien gesek statis berlaku pada gaya gesek statis yang bekerja pada benda membisu atau sempurna akan bergerak sedangkan koefisien gesek kinetis berlaku pada gaya gesek kinetis yang bekerja pada benda bergerak. Nah pada kesempatan kali ini, kita akan membahas wacana bagaimana caranya memilih rumus koefisien gesek (statis dan kinetis) pada benda yang terletak di bidang miring tanpa gaya luar. Namun, pertama-tama coba kalian amati dan pahami gambar ilustrasi berikut ini.
Sebuah balok bermassa m berada di bidang miring garang yang membentuk sudut sebesar θ terhadap arah horizontal. Diagram gaya-gaya yang bekerja pada balok diperlihatkan menyerupai pada gambar di atas. Berdasarkan gambar tersebut, ada dua komponen gaya yang bekerja pada sumbu-X yaitu w sin θ dan gaya gesek f. Oleh alasannya yakni itu, ada dua kemungkinan gerak benda, yaitu benda membisu atau benda bergerak ke bawah sejajar bidang miring.
Seperti yang telah dijelaskan sebelumnya, pada benda yang membisu maka gaya gesek yang bekerja yakni gaya gesek statis (fs = μsN) sedangkan pada benda yang bergerak, gaya gesek yang bekerja yakni gaya gesek kinetik (fk = μkN). Dengan demikian, besar koefisien gesek statis dan kinetik tersebut sanggup kita tentukan dengan memakai Hukum Newton khususnya Hukum I dan II Newton.
#1 Rumus Koefisien Gesek Benda yang Diam di Bidang Miring
Untuk benda yang membisu di atas bidang miring maka besar percepatannya yakni nol, sehingga berlaku Hukum I Newton sebagai berikut.
ΣFY = 0
N – w cos θ = 0
N – mg cos θ = 0
N = mg cos θ ………. Pers. (1)
ΣFX = 0
w sin θ – fs = 0
mg sin θ – μsN = 0
karena N = mg cos θ, maka
mg sin θ – μs(mg cos θ) = 0
mg sin θ – μsmg cos θ = 0
μsmg cos θ = mg sin θ
μs | = | mg sin θ |
mg cos θ |
Karena sin θ/cos θ = tan θ, maka
μs = tan θ ………. Pers. (2)
Dengan demikian, rumus koefisien gesek (statis) untuk benda yang membisu di bidang miring garang yakni sebagai berikut.
μs = tan θ |
#2 Rumus Koefisien Gesek Benda yang Bergerak di Bidang Miring
Untuk benda yang mula-mula membisu diatas bidang miring kemudian bergerak ke bawah sejajar bidang, maka pada benda berlaku Hukum II Newton sebagai berikut.
ΣFY = ma
N – w cos θ = ma
N – mg cos θ = ma
Karena tidak ada gerak dalam arah vertikal, maka a = 0 sehingga
N – mg cos θ = 0
N = mg cos θ ………. Pers. (3)
ΣFX = ma
w sin θ – fk = ma
mg sin θ – μkN = ma
karena N = mg cos θ, maka
mg sin θ – μk(mg cos θ) = ma
mg sin θ – μkmg cos θ = ma
μkmg cos θ = mg sin θ – ma
μk | = | g sin θ – a |
g cos θ |
Atau sanggup kita tuliskan sebagai berikut.
μk | = | tan θ | – | a | ………. Pers. (3) |
g cos θ |
Jadi, besarnya koefisien gesek (kinetis) pada benda yang bergerak di atas bidang miring sanggup kita tentukan dengan memakai persamaan berikut.
μk | = | tan θ | – | a | |
g cos θ |
Keterangan: | ||
N | = | Gaya Normal benda (N) |
w | = | Gaya berat benda (N) |
m | = | Massa benda (kg) |
θ | = | Sudut kemiringan bidang |
a | = | |
g | = | Percepatan gravitasi bumi (m/s2) |
#3 Contoh Soal Menentukan Koefisien Gesek
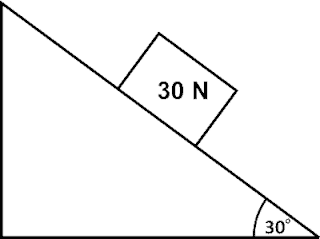
Sebuah benda dengan berat 30 N berada pada bidang miring, menyerupai yang diperlihatkan pada gambar di atas. Ternyata, benda sempurna akan meluncur ke bawah. Jika percepatan gravitasi bumi yakni 10 m/s2, tentukan koefisien gesek antara benda dengan bidang miring!
Penyelesaian:
Dari soal kita ketahui bahwa benda sempurna akan meluncur jadi benda belum bergerak, sehingga gaya gesek yang bekerja yakni gaya gesek statis. Untuk memilih koefisien gesek (statis), kita gunakan persamaan (2) sebagai berikut.
μs = tan θ
μs = tan (30o)
μs = 1/3 √3
lalu bagaimana jikalau kalian lupa dengan rumus koefisien gesek tersebut? Tenang saja, bagi kalian yang tidak suka menghafal rumus, masih ada metode manual untuk menuntaskan dilema di atas. Metode manual yang dimaksud yakni dengan memilih persamaan gerak benda menurut Hukum Newton. Langkah pertama yakni menggambar garis-garis gaya yang bekerja pada benda, yaitu sebagai berikut.
Karena benda belum bergerak, maka a = 0. Sehingga berlaku Hukum I Newton sebagai berikut.
ΣFY = 0
N – w cos 30o = 0
N = w cos 30o
ΣFX = 0
w sin 30o – fs = 0
w sin 30o – μsN = 0
μsN = w sin 30o
μsw cos 30o = w sin 30o
μs | = | sin 30o |
cos 30o |
μs | = | ½ |
½ √3 |
μs | = | 1/3 √3 |
Demikianlah artikel wacana cara memilih rumus koefisien gesek (statis dan kinetis) pada benda yang berada di bidang miring lengkap dengan gambar ilustrasi dan garis-garis gayanya serta pola soal dan pembahasan. Semoga sanggup bermanfaat untuk Anda. Apabila terdapat kesalahan tanda, simbol, abjad maupun angka dalam perhitungan mohon dimaklumi. Terimakasih atas kunjungannya dan hingga jumpa di artikel berikutnya.