Kumpulan Rumus Percepatan Dan Tegangan Tali Sistem Katrol Bahan Dinamika Translasi
Salah satu bentuk penerapan Hukum Newton wacana gerak ialah pada sistem katrol. Terdapat aneka macam model sistem katrol yang persamaan geraknya sanggup dijelaskan dengan memakai Hukum Newton. Ada sistem katrol tetap, katrol bebas, katrol di bidang datar, katrol di bidang miring maupun sistem katrol kombinasi antara katrol tetap dan bebas yang terletak di bidang datar atau bidang miring.
Blog ini telah memaparkan sebagian besar artikel wacana persamaan gerak benda-benda yang dihubungkan pada katrol di mana artikel-artikel tersebut sanggup kalian temukan pada label “percepatan dan gaya tegangan tali biar kalian sanggup gampang memakai rumusnya dalam menuntaskan duduk kasus fisika.
Catatan Penting:Keadaan katrol yang akan kita bahas dalam artikel ini ialah katrol licin serta massa katrol dan juga tali diabaikan sehingga tidak ada momen inersia yang menghipnotis gaya tegangan tali sistem.
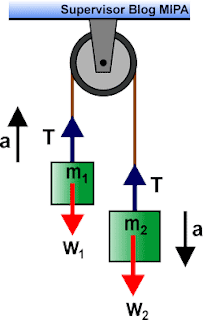
Dua benda bermassa m1 dan m2 digantungkan pada katrol tetap ibarat yang ditunjukkan pada gambar di atas. Jika m2 > m1 dan benda 1 bergerak ke atas serta benda 2 bergerak ke bawah dengan percepatan a, maka rumus percepatan dan gaya tegangan tali pada sistem ini ialah sebagai berikut.
a | = | (m2 – m1)g |
m1 + m2 |
T | = | 2m1m2g |
m1 + m2 |
Dua benda bermassa m1 dan m2 dihubungkan pada katrol tetap di mana benda 1 berada di bidang datar licin sedangkan benda 2 berada dalam posisi menggantung. Jika benda 1 bergerak ke kanan dan benda 2 bergerak ke bawah dengan percepatan sama sebesar a, maka rumus percepatan dan gaya tegangan tali pada sistem ini ialah sebagai berikut.
a | = | m2g |
m1 + m2 |
T | = | m1m2g |
m1 + m2 |
Dua benda bermassa m1 dan m2 dihubungkan pada katrol tetap di mana benda 1 berada di bidang datar agresif dengan koefisien gesek μ sedangkan benda 2 berada dalam posisi menggantung. Jika benda 1 bergerak ke kanan dan benda 2 bergerak ke bawah dengan percepatan sama sebesar a, maka rumus percepatan dan gaya tegangan tali pada sistem ini ialah sebagai berikut.
a | = | (m2 – μm1)g |
m1 + m2 |
T | = | (1 + μ)m1m2g |
m1 + m2 |
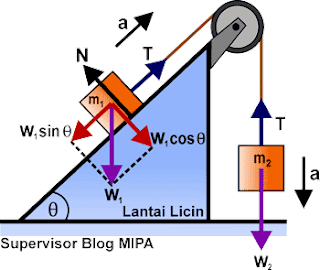
Dua benda bermassa m1 dan m2 dihubungkan pada katrol tetap di mana benda 1 berada di bidang miring licin yang membentuk sudut sebesar θterhadap arah horizontal sedangkan benda 2 menggantung. Jika benda 1 bergerak ke atas sejajar bidang dan benda 2 bergerak ke bawah dengan percepatan a, maka rumus percepatan dan gaya tegangan tali pada sistem ini ialah sebagai berikut.
a | = | (m2 – m1 sin θ)g |
m1 + m2 |
T | = | (1 + sin θ)m1m2g |
m1 + m2 |
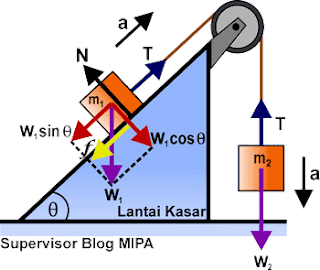
Dua benda bermassa m1 dan m2 dihubungkan pada katrol tetap di mana benda 1 berada di bidang miring agresif dengan sudut kemiringan sebesar θ dan besar koefisien gesek adalah μ sedangkan benda 2 menggantung. Jika benda 1 bergerak ke atas sejajar bidang dan benda 2 bergerak ke bawah dengan percepatan a, maka rumus percepatan dan gaya tegangan tali pada sistem ini ialah sebagai berikut.
a | = | (m2 – m1 sin θ – μm1 cos θ)g |
m1 + m2 |
T | = | (1 + sin θ + μ cos θ)m1m2g |
m1 + m2 |
Dua benda bermassa m1 dan m2 dihubungkan pada katrol tetap di mana benda 1 berada di bidang miring licin dengan sudut kemiringan α dan benda 2 berada di bidang miring agresif dengan sudut kemiringan β. Jika benda 1 bergerak ke atas dan benda 2 bergerak ke bawah sejajar bidang dengan percepatan a, maka rumus percepatan dan gaya tegangan tali pada sistem ini ialah sebagai berikut.
a | = | (m2 sin β – m1 sin α)g |
m1 + m2 |
T | = | (sin α + sin β)m1m2g |
m1 + m2 |
Dua benda bermassa m1 dan m2 dihubungkan pada katrol tetap di mana benda 1 berada di bidang miring agresif dengan sudut kemiringan α dan koefisien gesek sebesar μ1 sedangkan benda 2 berada di bidang miring agresif dengan sudut kemiringan β dan koefisien gesek sebesar μ1. Jika benda 1 bergerak ke atas dan benda 2 bergerak ke bawah sejajar bidang dengan percepatan a, maka rumus percepatan dan gaya tegangan tali pada sistem ini ialah sebagai berikut.
a | = | m2g(sin β – μ2 cos β) – m1g(sin α + μ1 cos α) |
m1 + m2 |
T | = | (sin α + sin β + μ1 cos α – μ2 cos β)m1m2g |
m1 + m2 |
Dua benda bermassa m1 dan m2 dihubungkan pada katrol tetap di mana benda 1 berada di bidang datar licin sedangkan benda 2 berada di bidang miring licin dengan sudut kemiringan θ. Jika benda 1 bergerak ke kanan dan benda 2 bergerak ke bawah sejajar bidang dengan percepatan a, maka rumus percepatan dan gaya tegangan tali pada sistem ini ialah sebagai berikut.
a | = | m2g sin θ |
m1 + m2 |
T | = | m1m2g sin θ |
m1 + m2 |
Dua benda bermassa m1 dan m2 dihubungkan pada katrol tetap di mana benda 1 berada di bidang datar agresif dengan koefisien gesek sebesar μ1sedangkan benda 2 berada di bidang miring licin dengan sudut kemiringan θ dan koefisien gesek sebesar μ2. Jika benda 1 bergerak ke kanan dan benda 2 bergerak ke bawah sejajar bidang dengan percepatan a, maka rumus percepatan dan gaya tegangan tali pada sistem ini ialah sebagai berikut.
a | = | (m2 sin θ – μ2m2 cos θ – μ1m1)g |
m1 + m2 |
T | = | (sin θ – μ2 cos θ + μ1)m1m2g |
m1 + m2 |